高中数学几何拓展试题

已知函数 $f\left(x\right)=A\sin (3x+\phi )(A＞0,x\in (-\infty ,+\infty ),0＜\phi ＜\pi ）$ 在x= $x=\frac{\mathrm{\pi }}{12}$ 时取得最大值4．．
（1）求 $f\left(x\right)$ 的最小正周期；
（2）求 $f\left(x\right)$ 的解析式；
（3）若 $f(\frac{2}{3}\alpha +\frac{\mathrm{\pi }}{12})=\frac{12}{5}$ ．求 $\tan 2\alpha$ 的值．

函数 $y=2\sin (2x+\frac{\mathrm{\pi }}{3})$， $x\in [-\frac{\mathrm{\pi }}{6},\frac{\mathrm{\pi }}{2}]$的值域是 ．

下列各式的大小关系正确的是（）

A．sin11°＞sin168°

B．sin194°＜cos160°

C．cos（﹣）＞cos

D．tan（﹣）＜tan（﹣）

已知函数f（x）=sinx+cosx．
（1）若f（x）=2f（﹣x），求的值；
（2）求函数F（x）=f（x）•f（﹣x）+f²（x）的最大值和单调递增区间．

命题p：关于x的不等式x²+2ax+4＞0，对一切x∈R恒成立，命题q：指数函数f（x）=（3﹣2a）^x是增函数，若p∨q为真，p∧q为假，求实数a的取值范围．

如图，在四边形ABCD中，已知AD⊥CD，AD=10，AB=14，∠BDA=60°，∠BCD="135°" 求BC的长．

关于命题p：A∩∅=∅，命题q：A∪∅=A，则下列说法正确的是（）

A．（￢p）∨q为假

B．（￢p）∧（￢q）为真

C．（￢p）∨（￢q）为假

D．（￢p）∧q为真

在△ABC中，a，b，c分别为角A，B，C所对边，若a=2bcosC，则此三角形一定是（）

A．等腰直角三角形

B．直角三角形

C．等腰三角形

D．等腰或直角三角形

已知函数 $f\left(x\right)={\sin }^{2}x+a\sin x\cos x-{\cos }^{2}x$，且 $f\left(\frac{\mathrm{\pi }}{4}\right)=1$.

（1）求常数a的值及 $f\left(x\right)$的最小值；
（2）当 $x\in \left[0,\frac{\mathrm{\pi }}{2}\right]$时，求 $f\left(x\right)$的单调增区间．

关于函数 $f\left(x\right)=4\sin (2x+\frac{\mathrm{\pi }}{3})(x\in R)$ ，有下列命题：
① $y=f\left(x\right)$ 的表达式可改写为 $y=4\cos (2x-\frac{\mathrm{\pi }}{6})$ ；
② $y=f\left(x\right)$ 是以 $2\pi$ 为最小正周期的周期函数；
③ $y=f\left(x\right)$ 的图象关于点 $\left(-\frac{\mathrm{\pi }}{6},0\right)$ 对称；
④ $y=f\left(x\right)$ 的图象关于直线 $x=-\frac{\mathrm{\pi }}{6}$ 对称．
其中正确的命题的序号是 ．

函数 $f\left(x\right)=\sin x$ , $(\frac{\mathrm{\pi }}{6}\le x\le \frac{2\mathrm{\pi }}{3})$ 的值域为 ．

已知函数f（x）=asinωxcosωx+cos²ωx（a＞0，ω＞0）的最小正周期为，最小值为﹣，将函数f（x）的图象向左平移φ（φ＞0）个单位后，得到的函数图象的一条对称轴为x=，则φ的值不可能为（）

A．

B．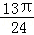

C．

D．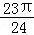

函数y=sin（2x+）的图象的一条对称轴的方程是（）

A．x=﹣

B．x=﹣

C．x=

D．x=

已知如图是函数y=2sin（ωx+φ）（|φ|＜）的图象，那么（）

A．ϖ=，φ=

B．ϖ=，φ=﹣

C．ϖ=2，φ=

D．ϖ=2，φ=﹣

将函数y=f（x）的图象沿x轴向左平移π个单位后，再将所得图象上各点的横坐标缩小为原来的一半，得到函数y=sinx的图象，那么y=f（x）的表达式为（）

A．y=sin2x

B．y=﹣sin2x

C．

D．