2011年2月21日,“雪龙”号极地考察船抵近南极中山站,考察船与中山站之间是一层海冰.科考队员打算驾驶履带车驶过冰层前往中山站,载人履带车的质量为25t,每条履带与冰面的接触面积为2m2.为探测冰层的承受极限,科考队员把质量为280kg、底面积为400cm2的钢锭压在水平冰层上,冰层恰好处于极限状态(有微小裂缝但无明显破裂).问:
⑴冰层能承受的极限压强是多少?(g取10N/kg)
⑵通过计算判断履带车能否安全驶过冰层?
一薄壁杯子装水后放在水平桌面上,水深0.1米,杯子的底面积是2×10-3米2,求杯底受到水的压强和压力。
小刚同学质量为60kg,双手倒立在地面上,每只手掌与地面的接触面积是150cm2(g=10N/kg)求:
(1)小刚的重力;
(2)小刚双手倒立时对地面的压强。
小刚同学质量为60kg,双手倒立在地面上,每只手掌与地面的接触面积是150cm2,(g=10N/kg)求:
(1)小刚的重力。
(2)小刚双手倒立时对地面的压强。
(3)某沼泽地能承受的最大压强为0.5×104Pa,他与某沼泽地接触时,接触面积多大才不会陷入该沼泽地?
五岳之首的泰山是我国著名的旅游胜地,人们可乘坐索道吊车观赏泰山美景(如图15所示)。据了解,中天门索道全长约2078m,上、下高度差约600m,单个吊车载满人后的总重是6000N。以单个吊车载满人为例,问:
(1)若吊车与索道的接触面积是0.02m2,索道承受的压强多大?
(2)若吊车从索道最高处运行到最低处需要10分钟,重力做功的功率是多大?
如图所示为抗震救灾自动化研究所研制的救援机器人,在雅安地震救援现场首次进行作业。若该机器人的质量为28 kg,履带与地面接触的总面积为0.7 m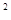 。
。
求:(1)该机器人的重力;
(2)该机器人对水平地面的压强。
按照规定,我国载货车辆的轮胎,对地面的压强应控制在700kPa(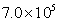 Pa)以内,但有些司机,为了获取更多利益,肆意超载。有一辆自重3t的6轮货车,核准载货量为4t,实际装货9t,如果每个车轮与路面的接触面积为0.02m2,每个车轮平均分担所有负重。(g取10N/kg)
Pa)以内,但有些司机,为了获取更多利益,肆意超载。有一辆自重3t的6轮货车,核准载货量为4t,实际装货9t,如果每个车轮与路面的接触面积为0.02m2,每个车轮平均分担所有负重。(g取10N/kg)
(1)通过计算说明,该车对路面的压强是否超过规定?
(2)运用所学的物理知识说明超载的危害(只要求说出两点)
如题19 图所示为某种型号潜水艇,其体积为5×103m3。
(海水密度近似取1.0×103kg/m3, g 取10N / kg)
求:(1)它在潜入到水下执行任务时所受浮力;
(2)当它潜入到水下200m 时,它的一个面积为1.2m2的舱盖所受海水的压强和压力。
如图所示,一个方桌(四只脚)重75 N,桌上放有一台质量为20 kg的电视机,桌子每只脚与水平地面的接触面积是25 cm2,求桌子对地面的压强.
“中国山西,晋善晋美”.为了倡导绿色出行,省城太原投放了大量的公共自行车.如图,小明在水平路面上骑行时,人与车总质量约70 kg,每个轮胎与地面接触面积约为100 cm2.
(1)此时自行车对地面的压强是多少?
(2)若小明以5 m/s的速度匀速骑行5 min,所受阻力是总重力的0.06倍,求出小明克服阻力做功的功率.
一辆质量为50t坦克停在水平地面上,履带与地面的接触面积是3m2.g=10N/kg,求:
(1)该坦克的重;
(2)该坦克对地面的压力和压强.
在世博会的建筑工地上,为了修建万花塔,用电动吊车将水泥板吊上塔顶。电动机正常工作50s,将质量为240kg、面积为1m2的水泥板匀速提升20m。电动机铭牌上标有“220V 2kW”字样,求:(g=10N/kg)
(1)水泥板水平放置在地面上时,对地面的压强?
(2)这段时间内,电动机消耗了多少电能?
(3)这段时间内,电动吊车的效率是多少?
洒水车在晨曦中辛勤的工作,已知汽车自重2.5吨,满载时装水10吨,共有10个轮胎,每个轮胎与地面的接触面积为0.05 m2,
(1)求汽车与水共重多少牛顿?
(2)洒水车在2分钟内沿平直街道匀速行驶600米,求洒水车的速度是多少米/秒?
(3)求装满水时,汽车对地面的压强是多少帕斯卡?
“中国山西,晋善晋美”.为了倡导绿色出行,省城太原投放了大量的公共自行车.如图,小明在水平路面上骑行时,人与车总质量约70 kg,每个轮胎与地面接触面积约为100 cm2.
(1)此时自行车对地面的压强是多少?
(2)若小明以5 m/s的速度匀速骑行5 min,所受阻力是总重力的0.06倍,求出小明克服阻力做功的功率.
放置在水平地面上的两个物体A和B均为实心长方体,它们的长、宽、高如下图所示。物体A的密度为0.8×103kg/m3,物体B的质量为8kg。求: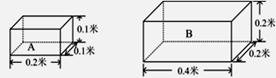
(1)物体A的质量;
(2)物体B所受重力的大小;
(3)在保持物体A、B原有放置方式的情况下,若沿竖直方向截取物体,并通过一定的方法使它们对水平地面的压强相等。下表中有两种方案,请判断这两种方案是否可行,若认为可行,计算所截取的长度。
| |
内 容 |
判断(填“行”或“不行”) |
| 方案一 |
从A的右侧截取一部分长方体叠放在B的上表面 |
|
| 方案二 |
分别从A、B的右侧按相同比例截取一部分长方体,叠放在对方剩余部分的上表面 |
|