初中物理压强和浮力试题

“嫦娥三号”探测器主要由两大部分构成：着陆器和巡视器，其中巡视器就是我们俗称“玉兔”的月球车（如图所示）。网上有许多学生和科学爱好者问了许多关于月球车的有趣问题，你能帮他回答吗？
（1）月球表面的某些部分土壤非常松软，而且崎岖不平，石块、陨石坑遍布。设计什么样的月球车轮才能方便它在月球表面行驶？
（2）月球车为什么不使用减震性能更好的充气轮胎？
（3）月球车的主要能量来源是什么？

以下是一则新闻消息：“今天零时，发改委将汽、柴油价格每吨分别降低125元和120元，测算到零售价格90号汽油和0号柴油每升分别降低0.09元和0.10元。……” 据此估测90号汽油的密度为（不考虑90号汽油生产过程中密度的变化）（  ）

A．0.80×10^3kg/m^3

B．0.75×10^3kg/m^3

C．0.72×10^3kg/m^3

D．0.70×10^3kg/m^3

如图所示，均匀圆柱体甲和盛有液体乙的圆柱形容器放置在水平地面上，甲、乙质量相等。现沿水平方向切去部分甲并从容器中抽取部分乙后，甲对地面的压强小于乙对容器底部的压强。若甲、乙剩余部分的体积分别是V_甲、V_乙，则（  ）

A．V甲可能等于V乙	B．V甲可能大于V乙
C．V甲一定大于V乙	D．V甲一定小于V乙

今年元旦，强降雪覆盖全国很多地区，导致交通、农业等民生问题受到严重影响，
(1)室外自来水水管有的被冻裂，原因是水管中的水结冰后体积     。（填“增大”、“减小”或“不变”）
(2)在活动中，除雪车发挥着重要的作用．如图所示是ZL300车，质量是5×10³kg，车轮与地面的总接触面积是0.25m²．除雪车对地面的压强是多少？

下列四个事例中，用于增大压强的是（       ）

A．推土机上安装两条履带	B．铁轨铺在枕木上
C．用滑雪板滑雪	D．把刀刃磨薄

为了将放置在水平地面上、重G="100" N的重物提升到高处。小明同学设计了图甲所示的滑轮组装置。当小明用图乙所示随时间变化的竖直向下拉力F拉绳时，重物的速度υ和上升的高度h随时间t变化的关系图像分别如图丙和丁所示。若重物与地面的接触面积S=5×10^-2 m²，不计摩擦，绳对滑轮的拉力方向均可看成在竖直方向。求：（1）、在2~3s内，拉力F的功率P及滑轮组的机械效率η？（2）、在1~2s内，拉力F做的功W？（3）、在0~1s内，重物对地面的压强P？

利用轮船上的电动机和缆绳从水库底竖直打捞出一长方体物体，下图P-t图像中表示了电动机输出的机械功率P与物体上升时间t的关系。已知0～80s时间内，物体始终以的速度匀速上升，当时，物体底部恰好平稳的放在轮船的水平甲板上。已知电动机的电压是200V，物体上升过程中的摩擦阻力不计，g取10N/kg。求：

（1）湖水的深度h₁，甲板离水面距离h₂ 。
（2）物体的质量m，长度，体积V 。
（3）若电动机电能转换为机械能的效率为80%，求在0～50s内，电动机线圈中电流的大小。

如图所示，试管A漂浮在水面上，试管B悬浮在水中。试管A与试管B都封闭有一定量的空气。以下说法正确的是：(     )

A将试管A上提一微小距离放手后试管A不会回到原来位置
B将试管A下压一微小距离，放手后试管A会回到原来位置
C将试管B上提一微小距离，放手后试管B会回到原来位置
D将试管B下压一微小距离，放手后试管B会回到原来位置

甲、乙两球的体积关系为V_甲=5V_乙，构成两球的物质的密度关系为ρ_乙=4ρ_甲，则两球的质量之比为    (    )

A．1:4

B．1:5

C．5：4

D．4:5

如图所示，A、B是两个完全相同的薄壁柱形金属容器，质量为0.5千克，底面积为0.01米²，容器高50厘米，分别装有2.0×10^﹣3米³的水和3.0×10^﹣3米³的酒精，置于水平桌面上（ ρ_酒精=0.8×10³千克/米³，g=10牛/千克）。求：

①水的质量。
②A容器对水平桌面的压强。
③ 请判断：当两个容器中的液体在增大同一深度△h后，容器中的液体对底部的压强能否达到p_水＞p_酒精？请通过计算说明理由。

如图甲所示，实心均匀正方体A、B放置在水平地面上，A的边长为0.2米，B的边长为0.3米，A的密度为3000千克/米，B的密度为2000千克/米．

（1）求正方体A的质量；
（2）求正方体B水平地面的压强；
（3）若正方体A、B在底部中间挖去厚度为h，底面积为0.01米的相同柱形后，如图乙所示，A、B剩余部分对水平地面的压强和．则、（选填“能”或“不能”）相等，请通过计算说明．

如图所示，三个底面积不同的圆柱形容器内分别盛有A、B、C三种液体，它们对容器底部的压强相等，现分别从三个容器内抽出相同深度的液体后，剩余液体对容器底部的压强、、的大小关系是

A．   B．
C．  D．

如图所示，质量均为2.4kg的薄壁圆柱形容器A和B放在水平地面上，底面积分别为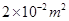和。容器A中盛有0.1m高的水，容器B中盛有质量为1.6kg的酒精。（ρ_酒精＝0.8×10³kg/m³）求：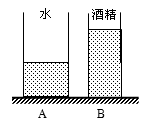

①容器B中酒精的体积V_酒精。
②容器B对水平地面的压强p_B。
③现有质量相等的甲、乙两实心物块，若将甲浸没在水中、乙浸没在酒精中后，两液体均未溢出，且两液体各自对容器底部压强的变化量相等，求甲、乙的密度ρ_甲、ρ_乙之比。

在图中，底面积不同的甲、乙圆柱形容器（S_甲>S_乙）分别装有不同的液体，两液体对甲、乙底部的压强相等。若从甲、乙中抽取液体，且被抽取液体的体积相同，则剩余液体对甲、乙底部的压力F_甲、F_乙与压强p_甲、p_乙的大小关系为 （    ）

A．F甲<F乙，p甲>p乙	B．F甲<F乙，p甲=p乙
C．F甲>F乙，p甲>p乙	D．F甲>F乙，p甲<p乙

如图3所示，放在水平地面上的均匀实心正方体甲、乙对地面的压强相等。现将两物体均沿水平方向切去一部分，则

A．若切去相等质量，甲被切去的厚度一定小于乙

B．若切去相等质量，甲被切去的厚度可能小于乙

C．若切去相等体积，甲对地面的压强一定小于乙

D．若切去相等体积，甲对地面的压强可能小于乙