初中物理压强和浮力试题

为了监测水库的水位，小明设计了利用电子秤显示水库水位的装置。该装置由长方体A和B、滑轮组、轻质杠杆CD、电子秤等组成，且杠杠始终在水平位置平衡，OC:OD=1:2，如图所示。

已知A的体积为0.03m³，A所受的重力600N,B所受的重力为110N；当水位上涨到与A的上表面相平时，水面到水库底部的距离h=20m。不计滑轮和绳的重力与摩擦。已知水的密度为1x10³kg/m³.求：
(l）水库底部受到水的压强；
(2)A受到的浮力；
(3）此时电子秤受到B对它的压力。

如图所示是一种电压力锅简易原理图,A为密闭锅体,锅盖面积为400cm²。R₁为工作时的加热电阻,L为指示灯,其电阻为20Ω,R₂为保温电阻,S₁为电源开关,S₂为压力开关，闭合S₁后，电路通过R₁对电力压力锅加热，当锅内气体压强达到设定值时，水开始沸腾，锅底向下移动，压力开关与触点a断开，并与 b点接通，起到控压控温的目的，此时保温电路的总功率为20W。

表一 水的沸点T与气体压强p 的关系
T/℃	100	105	110	112	114	116	118	120
p/kpa	101	121	143	154	163	175	187	199

 

表二 电压力锅的铭牌
额定电压	加热功率	压强设定值
220 V	1000W	175kpa

 
（1）当锅内121kpa时，锅内气体对锅盖的压力是多少？
（2）保温电阻R₂的阻值多大？
（3）已知锅内水的质量为m，初温为T₀、比热容为c，为了求出电压锅从开始加热到锅气压到设定值时的效率，只要测出闭合开关S₁到电路中        的时间为t，就可推导出效率的表达式η=           （用已知量表示）

由某种合金制成的两个大小不同的工艺品，其中一个实心，一个空心。小明为判定哪个是空心的，进行了如下实验。（已知ρ_水 = 1.0 g/cm³，取g = 10 N/kg）
【实验过程】将下列实验步骤中空白处补充完整。
①用弹簧测力计测出小工艺品的重力G₁ = 2 N。
②将挂在测力计下方的小工艺品浸没水中，小工艺品受到        个力的作用，此时测力计的示数F₁ = 1.6 N，则浮力F_浮 =            N。
③用测力计测出大工艺品的重力G₂ = 3 N。
④如图所示，将挂在测力计下方的大工艺品浸没水中，测力计的示数F₂ =           N。

⑤合金的密度ρ  =               g/cm³，则         （选填“大”或“小”）工艺品是空心的。
【拓展应用】空心工艺品空心部分的体积是          cm³。

利用轮船上的电动机和缆绳从水库底竖直打捞出一长方体物体，下图P-t图像中表示了电动机输出的机械功率P与物体上升时间t的关系。已知0～80s时间内，物体始终以的速度匀速上升，当时，物体底部恰好平稳的放在轮船的水平甲板上。已知电动机的电压是200V，物体上升过程中的摩擦阻力不计，g取10N/kg。求：
（1）湖水的深度h₁，甲板离水面距离h₂ 。
（2）物体的质量m，长度，体积V 。
（3）若电动机电能转换为机械能的效率为80%，求在0～50s内，电动机线圈中电流的大小。
 

如图（a）所示，实心正方体A、B放置在水平地面上，受到的重力分别为20牛和60牛，A的边长为0.2米，B的边长为0.3米．

①求正方体A对水平地面的压力F_A．
②求正方体B对水平地面的压强p_B．
③若在正方体A、B上分别放置与A、B底面积相等、材料相同的长方体物块C和物块D，如图（b）所示，如果它们的高度h相等，正方体A和B对水平地面的压强分别为p_A′和p_B′．请通过计算比较它们的大小关系及其对应的h的取值范围．

高压锅是家庭厨房中常见的炊具，利用它可以将食物加热到100℃以上．它省时高效，深受消费者欢迎．图（甲）为高压锅的构造，图（乙）为水的沸点与气压的关系图象．（g取10N/Kg，大气压为1标准大气压即10⁵Pa）．

（1）说出高压锅为什么能将食物加热到100℃以上？
（2）若高压锅出气孔的截面积约12mm²，压在出气孔上的安全阀的质量为84g．通过计算并对照图象说明利用这种高压锅烧水时，最高温度大约是多少？
（3）假若要把这种高压锅向西藏地区销售，用这种高压锅烧水时，要达到同样的最高温度，你认为需要做哪方面的改进，如何改进？

高压锅的锅盖通过几个牙齿似的锅齿与锅镶嵌旋紧，锅盖与锅之间有橡皮制的密封圈，不会漏气．锅盖中间有一排气孔，上面套着类似砝码的限压阀将排气孔堵住，当加热高压锅（锅内有水、食物），锅内气体压强增加到一定程度时．气体就会把限压阀顶起来，蒸气即可从排气孔排出锅外，这样就不会因为锅内压强过大而造成爆炸，以确保安全（如图1 0）．已知高压锅的限压阀的质量为100.8g，排气孔的面积为7mm²）．求：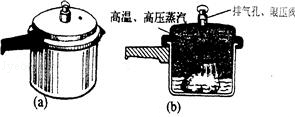

①锅内气体的压强最大可达多少？
②设锅内压强每增加3.6×10³P a，水的沸点就相应的增加1℃，则锅内的最高温度可达多高？（g取1 0N/k g：外界大气压强为1标准大气压，计算时取1×10⁵Pa）

放置在水平地面上的两个物体A和B均为质量分布均匀的实心正方体，正方体A的边长为0.1米，密度为0.8×10³千克/米³，正方体B的边长为0.2米，密度为0.5×10³千克/米³．求：
①正方体A对水平地面的压强．
②在保持正方体A、B原有放置方式的情况下，若沿竖直方向或者水平方向截取物体，使它们对水平地面的压强相等．表中有两种方案，请判断这两种方案是否可行，若认为可行，计算所截取的长度（或厚度）．

	内容	判断 （选填“行”或“不行”）
方案一	从正方体A的侧壁竖直截取一部分	不行
方案二	从正方体B的上方水平截取一部分	行

③计算截取的长度（或厚度）．

如图所示，底面积为200cm²的容器底部有一固定轻质弹簧，弹簧上方连有一边长为10cm的正方体木块A，容器侧面的底部有一个由阀门B控制的出水口，当容器中水深为20cm时，木块A有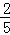的体积浸在水中，此时弹簧恰好处于自然状态，没有发生形变．（不计弹簧受到的浮力，g取10N/kg）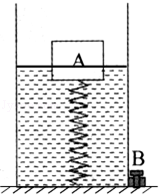   

求：（1）此时容器底部受到的水的压强；
（2）木块A的密度；
（3）向容器内缓慢加水，直至木块A刚好完全浸没水中，立即停止加水，弹簧伸长了3cm，求此时弹簧对木块A的作用力F₁是多大？容器底部受到水的压强变化了多少？

如图所示，在柱形容器内装有适量的水，水对容器底的压强为p，将质量为0.05kg的木块浸没在水中，用细线系在容器底，此时水对容器底的压强为1.5p，细线对木块的拉力是容器底所受水的压力的1/5，则木块的密度为　    　kg/m³．（g取10N/kg）

如图所示，边长为a、密度均匀的正方体物块静止于河岸边，在BB′边上施加一个力F使其绕DD′边转动掉落于河水中，它漂浮时露出水面的高度为h，水的密度为ρ，则下列说法中正确的是（　　）

A．物块的密度为

B．物块的重力为（a﹣h）ρga

C．物块漂浮在水面时底面受水的压强为ρg（a﹣h）

D．为了使物块掉落于河水中，力F至少是

小博想模拟同一艘轮船在海洋和河流中的沉浮情形．她将小铁块B固定在木块A上面代表“轮船”．用相同烧杯盛装等质量的水和盐水代表“河流”和“海洋”，放在水平桌面上，如图所示．第一次将AB放在水中，发现A的上表面恰好与液面相平；第二次放在盐水中，发现A的上表面露出了液面．则下面说法正确的是（　　）

A．由模拟实验可知，轮船由河流航行到海洋将下沉

B．AB在水中悬浮，在盐水中漂浮

C．AB在水中所受的浮力大于在盐水中所受的浮力

D．两烧杯底部所受液体的压力相等

如图所示，底面积不同的圆柱形容器A和B分别盛有甲、乙两种液体，两液面相平且甲液体的质量大于乙液体的质量．则此时液体对各自容器底部的压强p_A、p_B和液体对各自容器底部的压力F_A、F_B的关系是（　　）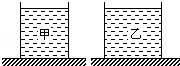

A．pA＜pB，FA=FB

B．pA＜pB，FA＞FB

C．pA＞pB，FA=FB

D．pA＞pB，FA＞FB

归纳式探究：
叶子探究在温度为0℃条件下，一定质量的氮气的压强和体积的关系．她将压强由1.013×l0⁵Pa增加到1.013×10⁸Pa的过程中，得到如下实验数据（其中a、b对氮气来说是常数）：

P/Pa	V/m^3	PV/Pa•m^3	/Pa•m^3
1.013×10^5	2.24×10^﹣2	2.3×10^3	2.3×10^3
1.013×10^7	2.24×10^﹣4	2.3×10^3	2.3×10^3
5.065×10^7	0.62×10^﹣4	3.1×10^3	2.3×10^3
1.013×10^8	0.46×10^﹣4	4.1×10^3	2.3×10^3

（1）由上述实验数据可以得到如下公式：　    　="K" （K为常数），其中K=　     　（写上单位）．由数据形式变为公式形式运用了　      　法．
（2）在压强由1.013×10⁵Pa增加到1.013×10⁷Pa的过程中，我们可以将公式简化为　   　，则这时的p﹣V关系可以用图象中的图线　      　来表示．

（3）实验中若氮气的压强为1.013×10⁶Pa，则它的体积为　        　．

如图所示，把同种材料制成的甲、乙两个正方体放在水平桌面上，甲、乙对桌面的压强分别为p₁、p₂．现把乙放在甲上，则甲对桌面的压强p为多少？（用p₁、p₂表示）