“塔吊”是北海新城区建设中随处可见的一种起重设备，图甲所示是某塔吊的工作示意图，AO是塔吊的平衡臂，BO是塔吊的吊臂，C为可控制移动的滑轮组小车，可在B点到O点间移动，AO长4m，BO长26m，AB可绕O点在一定的范围内上下倾斜，已知A端配重物的质量为5t，塔吊利用工作电压为380V、额定功率为10kW的电动机带动滑轮组来吊升工地的建筑材料．问：
（1）从安全角度出发，起吊时应尽量使吊臂水平平衡，在一次匀速吊升钢材时塔吊的吊臂如图乙所示，则滑轮组小车C应向 移动（选填“左”或“右”），这是根据 原理．
（2）将质量为2t的钢材以0.5m/s的速度竖直向上匀速提起，经1min到达施工楼层后再水平移动20m将钢材送到施工点，此过程中塔吊拉力对钢材所做的功是多少？
（3）此塔吊某次吊升钢材时，施工人员移动滑轮组小车C到达离O点16m处，使吊臂和平衡臂刚好处于水平平衡，电动机在额定功率下竖直向上匀速吊升钢材到某高度，此时电动机将电能转化为机械能的效率为75%，则钢材上升过程中的速度是多大？（吊臂、平衡臂、滑轮组的质量及摩擦力忽略不计）
如图所示，O为杠杆的支点，在杠杆的右端B点挂一重物。MN是以A为圆心的弧形导轨，绳的一端系在杠杆的A点，另一端E可以在弧形导轨上自由滑动。当绳的E端从导轨的一端N点向另一端M点滑动的过程中，杠杆始终水平，绳AE对杠杆拉力的变化情况：（ ）
| A．先变小，后变大 | B．先变大，后变小 |
| C．一直变小 | D．一直变大 |
图中，杠杆调平衡后，将两个体积相同的重物分别挂在杠杆两侧的A、B处，杠杆仍然平衡．则两重物重力大小之比GA：GB= ；若要将两重物同时浸没在水中，则杠杆的 端将上升．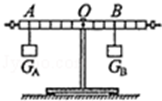
按照题目要求作图：
（1）在a图中，杠杆AB处于平衡状态，请作出细线对杠杆B点拉力F1的示意图、与力臂L对应的力F2的示意图
（2）如图所示，在该图中改动一根线，使L1、L2串联（在b图中完成），在该图中加一根线，使L1、L2并联（在c图中完成）。
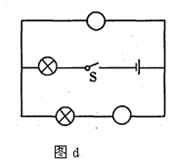
（３）如图d，在圆圈内填入正确的电表符号，使开关闭合后两灯都能发光．
如图甲所示，长1.6m、粗细均匀的金属杆可以绕O点在竖直平面内自由转动，一拉力﹣﹣位移传感器竖直作用在杆上，并能使杆始终保持水平平衡．该传感器显示其拉力F与作用点到O点距离x的变化关系如图乙所示．据图可知金属杆重（ ）
| A．5N | B．10N | C．20N | D．40N |
某同学想利用杠杆的平衡条件来测量刻度尺的质量。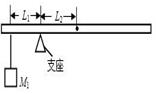
⑴将刻度尺平放在支座上，左右移动刻度尺，找出能够使刻度尺在水平位置保持平衡的支点位置，记下这个位置，它就是刻度尺的_______________；
⑵如图所示，将质量为M1的物体挂在刻度尺左边某一位置，向_____（选填“左” 或“右” ）移动刻度尺，直到刻度尺能够在支座上重新保持水平平衡。记录物体悬挂点到支座的距离L1和刻度尺的____________到支座的距离L2；
⑶根据杠杆的平衡条件，可以计算出刻度尺的质量m=__________（用所给物理量表示）。
(8分) 小明用质量忽略不计的杆秤测量物体M的质量，如图所示。当秤砣位于位置B时，杆秤在水平位置平衡。将物体浸没在纯水中，秤砣移至位置C时，杆秤在水平位置重新平衡。已知秤砣的质量为2kg， OB=5OA， OC=3OA，g=10N/kg，求：
（1）物体M的质量；
（2）物体浸没水中时受到的浮力；
（3）物体的密度。
杆秤是一种很古老但现在仍然在广泛使用的一种测量质量的工具。小林同学用一杆秤称一实心球的质量，如图所示。当杆秤在水平位置平衡时，秤砣拉线正好压在4 kg的刻度线上。根据秤砣拉线、提纽和称钩所在秤杆的位置之间的距离的粗略关系，可以估测出秤砣的质量大约是（ ）
| A．10g |
| B．400g |
| C．1000g |
| D．4000g |
杠杆的平衡条件是：____________________，一根杠杆，动力臂与阻力臂之比是5∶3，要使杠杆平衡，则动力和阻力之比为__________，这是一个__________杠杆（选填“省力”、“费力”或“等臂”）．
如图所示轻质杠杆，把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时，杠杆在水平位置平衡，若将甲物体浸没在水中，同时把支点从O移到O′时，杠杆又在新的位置平衡，若两次支点的距离O O′为OA的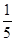
，求：甲、乙两个物体的质量之比．
如图，杠杆处于平衡状态，如果在杠杆两侧挂钩码处各增加一个质量相同的钩码，杠杆会
| A．左端下降 |
| B．右端下降 |
| C．仍然平衡 |
| D．无法判断 |
（1）如图所示是右侧带书柜的办公桌，我们可以把它抽象成一个“杠杆”．现在要用一个最小的力将这张办公桌的一端稍抬离地面．请画出这个力F和这个力臂l，并用“O”标明这个“杠杆”的支点．
（2）在右图中画出斜面上“不倒翁”受重力的示意图，并画出重力相对于支点Ｏ的力臂l 1． (黑点表示“不倒翁”的重心)
如图甲是小明根据“杠杆平衡条件”制作的只需要一个砝码的天平，横梁可绕轴O在竖直平面内转动，左侧为悬挂在固定位置P的置物盘，右侧所用砝码是实验室里常见的钩码，用细线挂在右侧带刻度线的横梁上．
（1）下面是小明测量物体质量的几个主要步骤，最合理的顺序是（只填写序号）
| A．将悬挂钩码的细线移到右侧横梁的零刻线Q处 |
| B．将天平放在水平台面上 |
| C．调整横梁右侧的平衡螺母使横梁上悬挂的重垂线对准底座上的标记 |
| D．将待测物体放在天平左侧的置物盘中 |
E．由细线在横梁上的位置对应的刻度值直接得出物体的质量
F．移动悬挂钩码的细线使横梁上悬挂的重垂线对准底座上的标记
（2）调节天平至水平位置平衡后，刚把待测物体放在天平左侧的置物盘中时，横梁上悬挂的重垂线将对准底座上标记的 侧（填“左”或“右”）；
（3）若某次测量最终达到平衡时钩码位于右侧横梁上的N处，如图乙所示，已知OP=L，OQ=d，ON=a，钩码质量为m，则待测物体的质量M= ．（用所给字母表示）
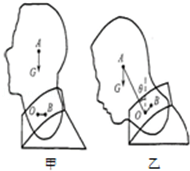
“低头族”长时间低头看手机，会引起颈部肌肉损伤．当头颅为竖直状态时，颈部肌肉的拉力为零，当头颅低下时，颈部肌肉会产生一定的拉力．为了研究颈部肌肉的拉力与低头角度大小的关系，我们可以建立一个头颅模型来模拟实验，如图甲所示．把人的颈椎简化成一个支点O，用1kg的头颅模型在重力作用下绕着这个支点O转动，A点为头颅模型的重心，B点为肌肉拉力作用点．将细线的一端固定在B点，用弹簧测力计拉着细线模拟测量肌肉的拉力，头颅模型在转动过程中，细线拉力的方向始终垂直于OB，如图乙所示．让头颅模型从竖直状态开始转动，通过实验记录出低头角度θ及细线拉力F的数据．如表：
| 低头角度θ/° |
0 |
15 |
30 |
45 |
60 |
| 细线拉力F/N |
0 |
7.3 |
14.0 |
20.2 |
25.0 |
（1）头颅模型质量为1kg，当低头角度为60°时，颈部肌肉实际承受的拉力是 N；如果真实头颅质量为8kg，当低头角度为60°时，颈部肌肉实际承受的拉力是 N．
（2）请解释：为什么低头角度越大，颈部肌肉的拉力会越大？答 ．
（3）请你就预防和延缓颈椎损伤提出一个合理化的建议： ．
如图所示，杠杆MN可绕O点转动，A、B、C、D是四个供人娱乐的吊环、B环到O点的距离为D环O点距离的一半，父子俩在吊环上做游戏，质量为40kg的儿子吊在B环上，父亲站在地面上抓着D环．（g=10N/kg）求：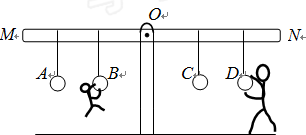
⑴ 若不计杠杆和吊环的重以及转轴间的摩擦，为使杠杆在水平位置平衡，父亲要用多大的力拉吊环D？
⑵ 若父亲实际使用竖直向下的拉力为250N，在4s内将儿子匀速拉高0.5m，父亲要做多少功？做功的功率多大？
⑶ 父亲提升儿子的过程中，该器材的机械效率为多少？
粤公网安备 44130202000953号