为安全起见，妈妈为小明买了一块浮板辅助练习游泳．妈妈认为浮板能漂在水面上是因为它轻，小明认为妈妈的说法不对，科学的说法是因为浮板的密度比水的密度小．为验证自己的说法，小明设计了如下实验：
（1）找一根轻质均匀木棍、细绳（质量忽略不计）和一块标有“净重115g”字样的新肥皂，用如图所示的方法进行测量．测量时，使木棍在 位置平衡，记下A、B的位置，用刻度尺测出OA=10cm，OB﹣40cm，则浮板的质量为 kg．
（2）把浮板压入装满水的桶中刚好浸没，用塑料袋（质量忽略不计）收集溢出的水，用（1）所述方法测得溢出水的质量为4.6kg，则浮板的体积为 m3，密度为 kg/m3；用刻度尺测肥皂的长、宽、厚，算出肥皂的密度为1.33×l03kg/m3．浮板在水中漂浮而肥皂在水中下沉，说明小明的说法是正确的．小明用此浮板游泳时浮板受到的最大浮力为 N．
（3）根据这个实验结果，妈妈说原来用密度比水小的材料制成的物体才能漂浮在水上，这种说法 （选填“正确”或“不正确”）．请举例说明 ．
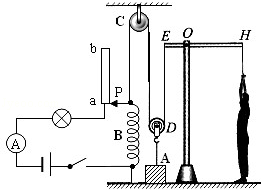
如图一均匀木板长12m，重200N，距A端3m处有一固定转轴O，另一端B用细绳悬吊着，使木板成水平状态．若细绳能承受的最大拉力为200N，细绳与木板的夹角为30°，欲使一个体重为600N的人在板上能安全行走，此人在板上行走的范围是多大？（求出离O点左侧多少米到离O点右侧多少米）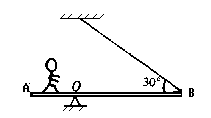
如图是液压汽车起重机从水中打捞重物的示意图．A 是动滑轮，B 是定滑轮，C 是卷扬机，D 是油缸，E是柱塞．作用在动滑轮上共三股钢丝绳，卷扬机转动使钢丝绳带动动滑轮上升提取重物，被打捞的重物体积V=0.5m3若在本次打捞前起重机对地面的压强p1=2.0×107Pa，当物体在水中匀速上升时起重机对地面的压强p2=2.375×107Pa，物体完全出水后起重机对地面的压强p3=2.5×107Pa．假设起重时柱塞沿竖直方向，物体出水前、后柱塞对吊臂的支撑力分别为N1和N2，N1与N2之比为19：24重物出水后上升的速度v=0.45m/s．吊臂、定滑轮、钢丝绳的重以及轮与绳的摩擦不计．（g取10N/kg）求：
（1）被打捞物体的重力；
（2）被打捞的物体浸没在水中上升时，滑轮组AB的机械效率；
（3）重物出水后，卷扬机牵引力的功率．
如图所示，一轻质杠杆支在支架上，OA=20cm， G1为边长是5cm的正方体，G2重为20N。当OC=l0cm时，绳子的拉力为 N，此时G1对地面的压强为2×104Pa。现用一水平拉力，使G2以 cm/s的速度向右匀速运动，经过12．5s后，可使G1对地面的压力恰好为0。
如图是某型号起重机从水中调起一重7.9t的钢锭，L1、L2分别为2m、6m。(g取10N／kg，ρ钢＝7.9×103kg／m3) 求：
（1）钢锭全部浸在水中时受到的浮力是多大?
（2）起重机将钢锭调离水面后，起重机的作用力F1是多大？
（3）调离水面后钢锭又匀速上升了3m，这个过程中起重机做的功为3.95×105J，这时，起重机的机械效率是多少？
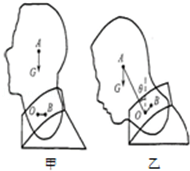
“低头族”长时间低头看手机，会引起颈部肌肉损伤．当头颅为竖直状态时，颈部肌肉的拉力为零，当头颅低下时，颈部肌肉会产生一定的拉力．为了研究颈部肌肉的拉力与低头角度大小的关系，我们可以建立一个头颅模型来模拟实验，如图甲所示．把人的颈椎简化成一个支点O，用1kg的头颅模型在重力作用下绕着这个支点O转动，A点为头颅模型的重心，B点为肌肉拉力作用点．将细线的一端固定在B点，用弹簧测力计拉着细线模拟测量肌肉的拉力，头颅模型在转动过程中，细线拉力的方向始终垂直于OB，如图乙所示．让头颅模型从竖直状态开始转动，通过实验记录出低头角度θ及细线拉力F的数据．如表：
| 低头角度θ/° |
0 |
15 |
30 |
45 |
60 |
| 细线拉力F/N |
0 |
7.3 |
14.0 |
20.2 |
25.0 |
（1）头颅模型质量为1kg，当低头角度为60°时，颈部肌肉实际承受的拉力是 N；如果真实头颅质量为8kg，当低头角度为60°时，颈部肌肉实际承受的拉力是 N．
（2）请解释：为什么低头角度越大，颈部肌肉的拉力会越大？答 ．
（3）请你就预防和延缓颈椎损伤提出一个合理化的建议： ．
如图所示，杠杆MN可绕O点转动，A、B、C、D是四个供人娱乐的吊环、B环到O点的距离为D环O点距离的一半，父子俩在吊环上做游戏，质量为40kg的儿子吊在B环上，父亲站在地面上抓着D环．（g=10N/kg）求：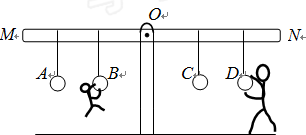
⑴ 若不计杠杆和吊环的重以及转轴间的摩擦，为使杠杆在水平位置平衡，父亲要用多大的力拉吊环D？
⑵ 若父亲实际使用竖直向下的拉力为250N，在4s内将儿子匀速拉高0.5m，父亲要做多少功？做功的功率多大？
⑶ 父亲提升儿子的过程中，该器材的机械效率为多少？
如图所示，平直的薄板AB长1m，重力忽略不计，B端用细绳悬于天花板上，绳与水平方向夹角为30°，薄板始终保持水平.一辆重20N、功率为1W的电动小车，从A端以0.2m/s的速度向右匀速行驶4s，细绳恰好被拉断，求：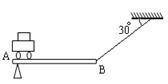
（1）小车行驶过程中牵引力做的功；
（2）小车运动时受到的阻力；
（3）细绳恰好被拉断时能承受的最大拉力.
如图所示轻质杠杆，把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时，杠杆在水平位置平衡，若将甲物体浸没在水中，同时把支点从O移到O′时，杠杆又在新的位置平衡，若两次支点的距离O O′为OA的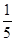
，求：甲、乙两个物体的质量之比．
一绝缘细绳的一端与可绕O点转动的轻质杠杆的E端相连，另一端绕过动滑轮D、定滑轮C，与滑动变阻器的滑片P相连；B为一可导电的轻质弹簧，如图所示接入电路中，一端通过绝缘绳固定在地面上，另一端与滑片P相连；一人站在地面上拉住与杠杆H端相连的细绳．已知电源电压为8V，灯泡标有"6V 3W"字样，人的质量为50kg，人与地面的接触面积为50cm 2，EO：HO=2：5．人对绳子拉力最小时，电流表示数为I1，且滑片刚好位于滑动变阻器的a端；人对绳子拉力最大时，电流表示数为I 2，且I 1：I 2=2：1，滑动变阻器的阻值与弹簧所受拉力的关系如下表所示：
| R（Ω） |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
… |
| F（N） |
0.5 |
50.5 |
100.5 |
150.5 |
200.5 |
250.5 |
300.5 |
350.5 |
… |
不计杠杆、弹簧、滑片、细绳的重力，不计摩擦，不计弹簧电阻．整套装置始终处于平衡状态，物体A始终不离开地面．灯泡电阻不变，且不会被烧坏．g=10N/kg．求：
（1）人的拉力最大时，滑动变阻器接入电路的阻值是多少？
（2）物体A的质量是多少？
（3）人的拉力最大时，人对地面的压强是多少？
（4）当灯泡正常发光时，物体A对地面的压力是多少？
如图所示，将边长为10cm的正方体合金块，用细绳挂在轻质杠杆的A点处，在B点施加力F1=30N时，杠杆在水平位置平衡，合金块对水平地面的压强恰好为0。撤去F1，在B点施加力F2时，合金块对地面的压强为1.2×103Pa。（OB=3OA，g取10N/kg）
（1）画出F2的力臂。
（2）求合金块的质量。
（3）求F2的大小。
某中学“STS”课题小组到某工厂的锅炉车间进行实践活动，重点研究锅炉供水自动控制装置方面的问题，如图为冷水自控位置，小水箱与锅炉相连，当杠杆呈水平状态时，浮球受到2.5N竖直向上的浮力，塞子B刚好顶住自来水的进口．已知OC=25cm．OD=1cm，塞子B横截面积为1cm2，由此算出自来水对塞子B的压强为多大？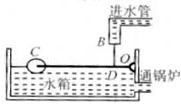
如图所示，质量为9kg，边长为5cm的正方体物块A置于水平地面上，通过细绳系于轻质杠杆BOC的B端，杠杆可绕O点转动，且CO=3BO，在C端用F=20N的力竖直向下拉杠杆，使杠杆在水平位置平衡，且细绳被拉直．（细绳重量不计，g取10N/kg）
求：（1）物体A的重力G1．
（2）B端细绳的拉力F拉；
（3）物体A对地面的压力F压；
（4）当F等于多少牛时，物体A对地面的压力恰好为零？
如图所示，一根轻质木杆，A端细线下所挂50N的重物静止在水平地面上。当在B点加竖直向下的力F=30N作用时，木杆恰能在水平位置处于平衡状态，此时细线竖直。已知OA=15cm，OB=5cm，OC=10cm，求：
（1）重物对水平地面的压力；
（2）在杠杆上找一点，在该点施加一个最小力，使重物对地面压力为0，在图中画出这个力并求出这个力的大小。
如图所示，起重机将一箱设备沿竖直方向匀速吊装到施工高台上，设备重4000 N，施工台距离地面的高度为3m。动滑轮上每段钢绳的拉力是2500 N。（取g=10N/kg）
求：（1）起重机的质量为8t，工作时用支架将汽车的轮胎支离开地面。如果地面能承受的最大压强是7×104 Pa，支架与地面接触的总面积是多少？
（2）起重臂OA长12m，且与水平方向夹角为30°。支撑臂与起重臂垂直，作用点为B，且OB=4m，求支撑臂给起重臂的支持力（忽略起重臂自重，cos30°≈0.87）。
（3）起重机做功的机械效率。
粤公网安备 44130202000953号