如图所示是某校九年级(10)班物理实验小组探究杠杆平衡条件的实验装置。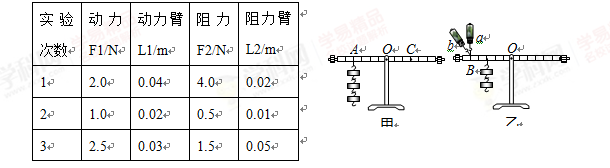
⑴实验前没有挂钩码时,小明同学发现杠杆右端下倾,则应将左端的平衡螺母向_____调。
⑵小华同学记录了三次实验数据如下表① 这三次实验数据中有一次是错误的,错误数据的实验次数是______,由正确实验结果可得杠杆的平衡条件是______。
②如图(甲)所示,当在A处挂了三个钩码时,要使杠杆平衡,应在C处挂______个钩码,(每个钩码的质量相等)。
③若某次实验中用弹簧测力计竖直向上拉杠杆一端的B点,如图乙所示,杠杆平衡时弹簧测力计的示数为Fa,若在B点斜向上拉,杠杆要求在水平位置再次平衡时,弹簧测力计的示数为Fb,则Fa ______ Fb (大于/小于/等于)。
(6分)⑴如图①所示,杠杆OA在力F1、F2的作用下处于静止状态,l2是力F2的力臂,请在图中画出力F1的力臂l1和力F2。
⑵在图②中,画出使轻质杠杆保持平衡的最小的力F的示意图(要求保留作图痕迹)。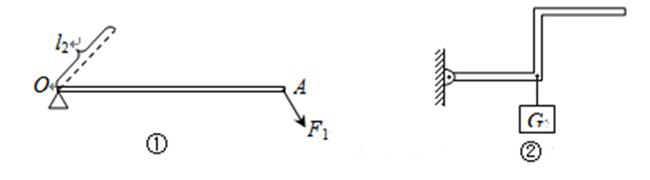
⑶按照左图所示的电路图,用笔画线代替导线,把右图中的实物连接起来,连线不要交叉。
如图甲所示,小明在探究“杠杆的平衡条件”实验中所用的实验器材有:杠杆、支架、弹簧测力计、刻度尺、细线和质量相同的钩码若干个。
(1)实验前,将杠杆中点置于支架上,当杠杆静止时,发现杠杆右端下沉。此时,应把杠杆两端的平衡螺母向 (选填“左”或“右”)调节,使杠杆在不挂钩码时,达到 位置平衡。
(2)杠杆调节平衡后,小明在杠杆上A点处挂4个钩码,在B点处挂6个钩码杠杆恰好在原位置平衡。于是小明便得出了杠杆的平衡条件为: 。他这样得出的结论是否合理? ;为什么? 。
(3)实验时只有8个相同的钩码,杠杆上每格等距,如图甲,当在A点挂4个钩码时,则怎样挂钩码可以使杠杆在水平位置平衡?_______
(4)实验结束后,小明提出了新的探究问题:“若支点不在杠杆的中点时,杠杆的平衡条件是否仍然成立?”于是小组同学利用如图乙所示装置进行探究,发现在杠杆左端的不同位置,用弹簧测力计竖直向上拉使杠杆处于平衡状态时,测出的拉力大小都与杠杆平衡条件不相符。其原因是: 。
(5)杠杆不处于水平位置能否平衡?甲乙意见不同。甲认为能平衡。于是他让每次杠杆倾斜时静止,做这个实验也得出了杠杆平衡条件。甲认为杠杆平衡不一定是水平的,这种说法对吗? (选填对或错),甲这种方案与乙让杠杆在水平位置做实验的方案相比较,你认为哪个实验方案好,并说明理
由: 实验方案好;理由是 。
如图,一块厚度、密度均匀的长方形水泥板放在水平地面上,用一竖直向上的力,欲使其一端抬离地面。则( )
| A.F甲>F乙,因为甲方法的动力臂长 |
| B.F甲<F乙,因为乙方法的阻力臂长 |
| C.F甲>F乙,因为乙方法时阻力臂短 |
| D.F甲=F乙,因为动力臂都是阻力臂的2倍 |
用不等臂的天平来称量某物体,当氢物体放在左盘里,往右盘加m1的砝码时天平平衡;当把同一物体放在右盘里,往左盘里加m2的砝码时,天平平衡。试根据杠杆平衡条件证明:物体的实际质量: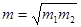
如图所示,轻质杠杆OA中点悬挂重为60N的物体,在A端施加一竖直向上的力F,杠杆在水平位置平衡,则力F的大小是 ____ N,保持F的方向不变,将杠杆从A位置匀速提升到B位置的过程中,力F将 ___ (变大/变小/不变)。
如图所示,为一可绕O点转动的杠杆,在A端通过绳作用一竖直向下的拉力F使杠杆平衡,此时AB部分水平,保持重物静止不动,而使绳绕A点从如图所示的位置沿图中的虚线CD转动,则( )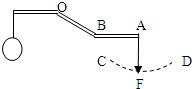
| A.逆时针转,F先变小后变大 |
| B.顺时针转,F先变小后变大 |
| C.顺时针转,F先变大后变小 |
| D.逆时针转,F先变大后变小 |
有一斜面长为L,高为h,现用力F沿斜面把物重为G的物体从底端匀速拉到顶端。已知物体受到斜面的摩擦力为f,则下列关于斜面机械效率η的表达式正确的是
A.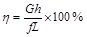 |
B.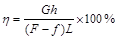 |
C.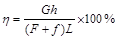 |
D.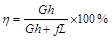 |
如图所示,一根轻质木杆,A端细线下所挂50N的重物静止在水平地面上。当在B点加竖直向下的力F=30N作用时,木杆恰能在水平位置处于平衡状态,此时细线竖直。已知OA=15cm,OB=5cm,OC=10cm,求:
(1)重物对水平地面的压力;
(2)在杠杆上找一点,在该点施加一个最小力,使重物对地面压力为0,在图中画出这个力并求出这个力的大小。
如图,杠杆处于平衡状态,如果在杠杆两侧挂钩码处各增加一个质量相同的钩码,杠杆会
| A.左端下降 |
| B.右端下降 |
| C.仍然平衡 |
| D.无法判断 |
(1)如图所示是右侧带书柜的办公桌,我们可以把它抽象成一个“杠杆”.现在要用一个最小的力将这张办公桌的一端稍抬离地面.请画出这个力F和这个力臂l,并用“O”标明这个“杠杆”的支点.
(2)在右图中画出斜面上“不倒翁”受重力的示意图,并画出重力相对于支点O的力臂l 1. (黑点表示“不倒翁”的重心)
如图甲是小明根据“杠杆平衡条件”制作的只需要一个砝码的天平,横梁可绕轴O在竖直平面内转动,左侧为悬挂在固定位置P的置物盘,右侧所用砝码是实验室里常见的钩码,用细线挂在右侧带刻度线的横梁上.

(1)下面是小明测量物体质量的几个主要步骤,最合理的顺序是(只填写序号)
| A.将悬挂钩码的细线移到右侧横梁的零刻线Q处 |
| B.将天平放在水平台面上 |
| C.调整横梁右侧的平衡螺母使横梁上悬挂的重垂线对准底座上的标记 |
| D.将待测物体放在天平左侧的置物盘中 |
E.由细线在横梁上的位置对应的刻度值直接得出物体的质量
F.移动悬挂钩码的细线使横梁上悬挂的重垂线对准底座上的标记
(2)调节天平至水平位置平衡后,刚把待测物体放在天平左侧的置物盘中时,横梁上悬挂的重垂线将对准底座上标记的 侧(填“左”或“右”);
(3)若某次测量最终达到平衡时钩码位于右侧横梁上的N处,如图乙所示,已知OP=L,OQ=d,ON=a,钩码质量为m,则待测物体的质量M= .(用所给字母表示)
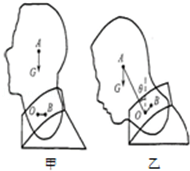
“低头族”长时间低头看手机,会引起颈部肌肉损伤.当头颅为竖直状态时,颈部肌肉的拉力为零,当头颅低下时,颈部肌肉会产生一定的拉力.为了研究颈部肌肉的拉力与低头角度大小的关系,我们可以建立一个头颅模型来模拟实验,如图甲所示.把人的颈椎简化成一个支点O,用1kg的头颅模型在重力作用下绕着这个支点O转动,A点为头颅模型的重心,B点为肌肉拉力作用点.将细线的一端固定在B点,用弹簧测力计拉着细线模拟测量肌肉的拉力,头颅模型在转动过程中,细线拉力的方向始终垂直于OB,如图乙所示.让头颅模型从竖直状态开始转动,通过实验记录出低头角度θ及细线拉力F的数据.如表:
| 低头角度θ/° |
0 |
15 |
30 |
45 |
60 |
| 细线拉力F/N |
0 |
7.3 |
14.0 |
20.2 |
25.0 |
(1)头颅模型质量为1kg,当低头角度为60°时,颈部肌肉实际承受的拉力是 N;如果真实头颅质量为8kg,当低头角度为60°时,颈部肌肉实际承受的拉力是 N.
(2)请解释:为什么低头角度越大,颈部肌肉的拉力会越大?答 .
(3)请你就预防和延缓颈椎损伤提出一个合理化的建议: .