初中物理探究杠杆的平衡条件实验计算题

已知斜面倾角为30°，斜面高为2m。小兵同学用绳子沿斜面将重为400N的木箱由斜面底端匀速拉到顶端。拉力大小为300N，绳重不计。求：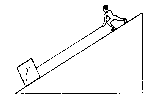

（1）小兵对木箱做的有用功；
（2）斜面的机械效率；
（3）斜面对物体施加的摩擦力。

杠杆平衡时，动力F₁的大小为10牛，动力臂l₁为0.2米，阻力臂l₂为0.1米，求阻力F₂的大小。

如图甲所示OA＝30cm，OC=60cm，利用弹簧测力计把一质量为0.5kg的物体以2cm/s的速度匀速提高10cm，弹簧测力计上升了20cm。弹簧测力计的拉力如图乙。（g=10N/kg）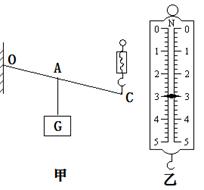

①弹簧测力计做了多少有用功？
②杠杆的机械效率是多少？
③拉力做功的功率是多少？

如图所示，一轻质杠杆可绕O点转动，在杠杆的A端挂一重为60牛的物体甲，在B端施加一个力F，已知OA∶AB＝1∶2。
求：为使杠杆水平平衡，作用在B端的力F的最小值和方向。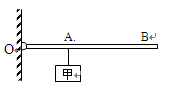

如图所示，轻质木板OB可绕O点转动，OB长1m，细线AB能承受的最大拉力为60N，在C点放一重为50N的物体M，OC长10cm，此时木板在水平位置处于静止状态。现在物体M上再加一水平向右的拉力F，使物体M在木板上匀速向右移动，经过5s细线AB断裂。若F的大小为10N。求：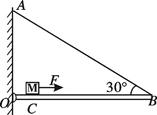

（1）物体M受到的滑动摩擦力；
（2）当AB断裂时M距O点的距离；
（3）5s内拉力做的功和拉力F的功率。

小明在探究利用杠杆做功的实践活动中，把重G为15N的重物挂在杠杆的中点，用手竖直提起棒的一端，使物体缓慢匀速提升，如图所示．
（1）不计杠杆自身重力和摩擦，求拉力F的大小？
（2）如杠杆是一根重为5N、质量均匀的硬棒，若在2s内将重物提升了0.1m，则小明使用杠杆所做的有用功是多大？机械效率是多大？拉力的功率是多大？

如图一均匀木板长12m，重200N，距A端3m处有一固定转轴O，另一端B用细绳悬吊着，使木板成水平状态．若细绳能承受的最大拉力为200N，细绳与木板的夹角为30°，欲使一个体重为600N的人在板上能安全行走，此人在板上行走的范围是多大？（求出离O点左侧多少米到离O点右侧多少米）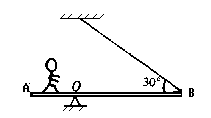

．如图所示，斜面长S＝6m，高h＝2.lm．用沿斜面方向50N的推力F，在10s内将一个重为100N的物体由斜面底端匀速推到顶端．求：

（1）推力F的功率：
（2）运动过程中物体克服摩擦力所做的功：
（3）斜面的机械效率．

如图，杠杆上标有刻度，G_A=15N，G_B＝8N，杠杆水平平衡时，A物体对杠杆的拉力是多少牛顿？ 此时A物体受到地面对它的支持力为多少？

如图所示．“塔吊”是建筑工地上普遍使用的起重设备．OC段为平衡臂，C端装有配重体，质量为1t，OD段叫吊臂，E处装有起吊重物的滑轮组，可在O、D两点间移动．其中OC=12m，OE=15m，OD=25m．滑轮组重力及摩擦忽略不计．（g取10N/kg）

（1）塔吊底座是由混凝土构件和砂、石、土等固体散料共同组成，组合后底面积大且质量也较大．
解释：底座面积大是为了　                 　；底座质量大是为了　                    　．
（2）当滑轮组在E、D两点间移动的过程中，用此“塔吊”能起吊重物的最大质量是多少？
（3）在某次施工过程中，工人师傅用“塔吊”在30s内把重为6000N的建筑材料提升到15m高处，“塔吊”对物体做功的功率是多少？

用不等臂的天平来称量某物体，当物体放在左盘里，往右盘加m₁的砝码时天平平衡；当把同一物体放在右盘里，往左盘里加m₂的砝码时，天平平衡。试根据杠杆平衡条件证明：物体的实际质量：

如图是锅炉上的保险阀，当阀门受到的蒸汽压强超过安全值时，阀门被顶开，蒸汽跑出一部分，使锅炉内的蒸汽压强减小，已知杠杆重可以忽略不计，OA与AB长度的比值为1∶3，阀门的面积是3 cm²，要保持锅炉内、外气体的压强差是1.2×10⁵ Pa，应将质量为多大的重物挂在杠杆的B点？（g取10 N/kg）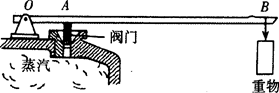

2012年6月我国自主研制的“蛟龙号”载人深潜器成功完成7000m深海探测，最大下潜深度7062米。如图甲所示，母船正在向海中投放“蛟龙号”，调控两根伸缩杆，使“∩”形架绕固定在甲板上的转轴转动至图甲所示位置时停止，然后由固定在“∩”形架顶部的绞车通过钢缆释放深潜器。处在图甲所示位置的“∩”形架可以简化为图乙中以O为支点的杠杆，OB表示“∩”形架，CD表示两根伸缩杆，O到CD的距离为2m，OD、OE的长度分别为3m、6m。深潜器的质量为25t，总体积为24.5m³。（不考虑“∩”形架、两根伸缩杆和绞车的重力，设海水的密度ρ_海水=1.0×10³kg/m³且不变）。

（1）“蛟龙号”所受重力是多少？
（2）“蛟龙号”达到最大下潜深度时，所受海水的压强是多少？
（3）在绞车匀速向下释放“蛟龙号”至刚浸没的过程中，钢缆BE起吊拉力的功率随时间变化的图象如图丙所示，图中P₁＝2P₂。求t₁时刻伸缩杆CD所受的拉力(不考虑水的阻力)。

如图装置为某学生在科技创新大赛时发明的可以直接测量液体密度的“密度天平”.其制作过程和原理如下：选择一根长l 米的杠杆，调节两边螺母使杠杆在水平位置平衡，在左侧离中点10厘米的A位置用细线固定一个质量为150克、容积为80毫升的容器。右侧用细线悬挂一质量为50克的钩码（细线的质量忽略不计）。测量时往容器中加满待测液体，移动钩码使杠杆在水平位置平衡，在钩码悬挂位置直接读出液体的密度。

(l）该“密度天平”的“零刻度”应标在右端离支点O_________厘米处；
(2）该“密度天平”的量程为多大？
(3）若将钩码的质量适当增大，该“密度天平”的量程将______________（选填“增大”“减小”或“不变”)

一把杆秤不计自重，提纽到秤钩距离是3cm，秤砣质量250g。用来称质量是2kg的物体，秤砣应离提纽多远，杆秤才平衡？若称量某物体质量平衡时，秤砣距提纽60cm，该物体质量多大？