如图所示，一根质量分布均匀的木棒，质量为m,长度为L，竖直悬挂在转轴O处。在木棒最下端用一方向始终水平向右的拉力F缓慢将木棒拉动到竖直方向夹角为θ的位置（转轴处摩擦不计）。问：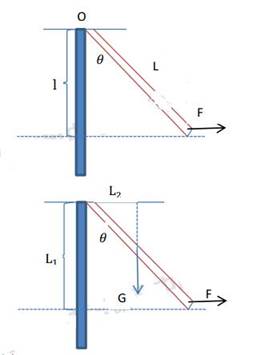
（1）在答题纸上画出θ=60°时拉力F的力臂L1，并计算力臂的大小。
（2）木棒的重力作用点在其长度二分之一处，随拉开角度θ的增加，拉力F将如何变化？
并推导拉力F与角度θ的关系式。
如图所示，将边长为10cm的正方体合金块，用细绳挂在轻质杠杆的A点处，在B点施加力F1=30N时，杠杆在水平位置平衡，合金块对水平地面的压强恰好为0。撤去F1，在B点施加力F2时，合金块对地面的压强为1.2×103Pa。（OB=3OA，g取10N/kg）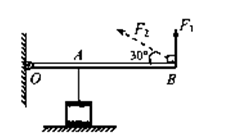
（1）画出F2的力臂。
（2）求合金块的质量。
（3）求F2的大小。
在图中画出使杠杆在水平位置平衡时作用在B点的最小力F的示意图（保留作图痕迹）．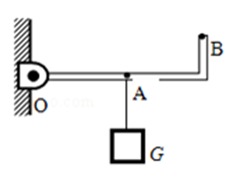
如图所示，起重机将一箱设备沿竖直方向匀速吊装到施工高台上，设备重4000 N，施工台距离地面的高度为3m。动滑轮上每段钢绳的拉力是2500 N。（取g=10N/kg）
求：（1）起重机的质量为8t，工作时用支架将汽车的轮胎支离开地面。如果地面能承受的最大压强是7×104 Pa，支架与地面接触的总面积是多少？
（2）起重臂OA长12m，且与水平方向夹角为30°。支撑臂与起重臂垂直，作用点为B，且OB=4m，求支撑臂给起重臂的支持力（忽略起重臂自重，cos30°≈0.87）。
（3）起重机做功的机械效率。
后端挑着装满道具的“百宝箱”，前端挑着由活动支架与花布组成的“戏台”，江西省非物质文化遗产传承人肖秋林就这样挑着担子四处游走，表演了40多年“一人一台戏”的布袋木偶戏。如图所示，假设“戏台”重100N，装了道具的“百宝箱”重200N，它们的悬挂点之间距离为l.5m，扁担视作重力不计的硬直棒。
（1）挑起担子时，“百宝箱”被提高了0.6m，这一过程中，需要克服“百宝箱”重力做多少功?
（2）假设肩膀与扁担的接触点为D，当手不对扁担施加力的作用时，要使扁担在水平位置平衡，前端悬挂点A与O点的距离多大?
（3）当前端的“戏台”卸下后，左手在A点施加力，同样能使扁担在水平位置平衡。若肖师傅是在站立时卸下“戏台”，则卸下“戏台”前后：
①扁担对肩膀压力 （填“变大”、“变小”或“不变”）。
②肖师傅对水平地面的压强如何变化?变化多大?（假设肖师傅的每只脚与地面的接触面积为200cm2）
如图是某型号起重机从水中调起一重7.9t的钢锭，L1、L2分别为2m、6m。(g取10N／kg，ρ钢＝7.9×103kg／m3) 求：
（1）钢锭全部浸在水中时受到的浮力是多大?
（2）起重机将钢锭调离水面后，起重机的作用力F1是多大？
（3）调离水面后钢锭又匀速上升了3m，这个过程中起重机做的功为3.95×105J，这时，起重机的机械效率是多少？
如图所示是一种起重机的简图，用它把质量为4×103㎏，底面积为1㎡的货物G匀速提起。(取g=10N／㎏)问：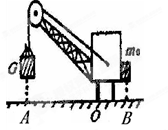
(1)若把货物匀速吊起10m，则起重机对货物做了多少功?
(2)若起重机在此过程中，用了20s的时间，则起重机对货物的拉力的功率多大？
(3)吊起货物时，为使起重机不翻倒，其右边至少要配一个质量为多大的物体?已知OA=10m，OB="5m" (起重机本身重力不计)
如图所示轻质杠杆，把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时，杠杆在水平位置平衡，若将甲物体浸没在水中，同时把支点从O移到O′时，杠杆又在新的位置平衡，若两次支点的距离O O′为OA的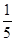
，求：甲、乙两个物体的质量之比．
如图所示，一根轻质木杆，A端细线下所挂50N的重物静止在水平地面上。当在B点加竖直向下的力F=30N作用时，木杆恰能在水平位置处于平衡状态，此时细线竖直。已知OA=15cm，OB=5cm，OC=10cm，求：
（1）重物对水平地面的压力；
（2）在杠杆上找一点，在该点施加一个最小力，使重物对地面压力为0，在图中画出这个力并求出这个力的大小。
如图所示，质量为9kg，边长为5cm的正方体物块A置于水平地面上，通过细绳系于轻质杠杆BOC的B端，杠杆可绕O点转动，且CO=3BO，在C端用F=20N的力竖直向下拉杠杆，使杠杆在水平位置平衡，且细绳被拉直．（细绳重量不计，g取10N/kg）
求：（1）物体A的重力G1．
（2）B端细绳的拉力F拉；
（3）物体A对地面的压力F压；
（4）当F等于多少牛时，物体A对地面的压力恰好为零？
如图所示，杠杆MN可能绕O点转动，A、B、C、D是四个供人娱乐的吊环、B环到O点距离为D环O点距离的一半，父子俩在吊环上做游戏，质量为40kg的儿子吊在B环上，父亲站在地面上抓着D环，用250N竖直向下的力在4s内把儿子拉高了0.5m．求：（g=10N/kg）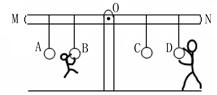
（1）父亲做的总功；
（2）父亲做功的功率；
（3）该器材的机械效率．
(8分) 小明用质量忽略不计的杆秤测量物体M的质量，如图所示。当秤砣位于位置B时，杆秤在水平位置平衡。将物体浸没在纯水中，秤砣移至位置C时，杆秤在水平位置重新平衡。已知秤砣的质量为2kg， OB=5OA， OC=3OA，g=10N/kg，求：
（1）物体M的质量；
（2）物体浸没水中时受到的浮力；
（3）物体的密度。
小军健身用的拉力器结构如图所示．他用250N的拉力向下拉动拉杆，使200N的配重块在 2s内匀速升高40cm．不计拉杆和绳的重力，g取10N/kg．求：
（1）克服配重的重力所做的功；
（2）拉力做功的功率；
（3）此过程中拉力器的机械效率．
过去农村用的舂米工具是一个杠杆，下图是它的结构示意图。O为固定转轴，在A端连接着石球，脚踏B端可以使石球升高，抬起脚，石球会落下击打稻谷。若石球重50N，要将石球抬起，脚至少用多大竖直向下的力？（摩擦和杠杆自重均忽略不计）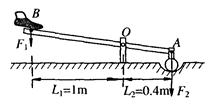
郝强同学对建筑工地上的长臂吊车（如图甲）有些疑惑：不吊物体它能平衡，吊重物也能平衡，重物沿臂移动仍能平衡！后来他通过设计“移动支点式杠杆”模型（如图乙）弄懂了类似问题：密度及粗细都均匀的直棒AB=1.8m，放在一个宽度为40cm的凳子上，当在棒的A端固定一个铅块（忽略大小）m铅=2kg时，棒刚好绕O1点有转动的趋势（AO1=30cm）．
（1）求棒的质量m棒；
（2）当在P处挂一重物时（PB=10cm），棒刚好绕O2点有转动的趋势．求重物质量m物及此时棒对O2点的压力F（g取10N/kg）；
（3）当悬线带着重物缓慢向A端移动时，可以认为凳面上只有某点E（即新支点）对棒有支持力．回答：随着重物左移，E点将“左移”或“右移”还不“不动”？棒对E点的压力FE是“变大”或“变小”还是“不变”？（不必说明理由）
粤公网安备 44130202000953号