如图所示，金属圆柱体甲的高度为d，底面积为S；薄壁圆柱形容器乙的底面积为2S，且足够高，其中盛有深度为H（H＞d）的液体，置于水平面上。
①若甲的体积为1×10（3米3，密度为2×103千克/米3，求它的质量m。
②若乙所受重力为G1，其中所装液体重为G2，求乙对水平面的压强p。
③现将甲浸入乙的液体中，其下表面所处深度为h，求液体对甲下表面压强p甲与液体对乙底部压强p乙的比值及其对应h的取值范围。
一带阀门的圆柱形容器，底面积是200cm2，装有12cm深的水，正方体M边长为10cm，重20N，用细绳悬挂放入水中，有
的体积露出水面，如图所示，试求：
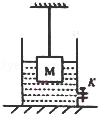
（1）正方体M的密度；
（2）正方体M受到的浮力以及此时水对容器底部的压强；
（3）若从图示状态开始，通过阀门K缓慢放水，当容器中水面下降了2cm时，细绳刚好被拉断，则细绳能承受的最大拉力是多少？（g取10N/kg，水的密度为1.0×103kg/m3）
如图所示，甲、乙两个均匀实心正方体分别放置在水平地面上，且它们各自对地面的压强相等。若分别在两个正方体的上部，沿水平方向截去相同高度后，则甲、乙的剩余部分对地面的压强P以及剩余部分质量m的大小关系为
| A．P甲＜P乙m甲＜m乙 | B．P甲＞P乙 m甲＞m乙 |
| C．P甲＜P乙m＞甲m乙 | D．P甲＞P乙 m甲＝m乙 |
三个相同的杯子中装有部分水，把质量相同的实心铜块、铁块、铝块依次放入甲、 乙、丙三个杯中，水面恰好相平，则原来装水最多的杯子是（ρ铜＞ρ铁＞ρ铝）（ ）
| A．甲杯 | B．乙杯 |
| C．丙杯 | D．原来装水一样多 |
体积为30cm3的空心铜球，它的质量为89g，现在用某种金属注满它的空心部分后球的质量变为245g．求这种金属的密度是多少？（ρ铜=8.9×103kg/m3）
一个不规则的实心物体，质量55g，放入装满纯水的烧杯中，沉入底部，排开0.5N的水．然后向烧杯中加盐并搅拌，直到物体悬浮为止．（g＝10N/kg)求：
（1)物体在纯水中所受的浮力；
（2)物体的体积；
（3)物体悬浮时盐水的密度．
如图所示轻质杠杆，把密度均为4.0×103kg/m3的甲、乙两个实心物体挂在A、B两端时，杠杆在水平位置平衡，若将甲物体浸没在水中，同时把支点从O移到O′时，杠杆又在新的位置平衡，若两次支点的距离O O′为OA的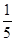
，求：甲、乙两个物体的质量之比．
自制潜水艇模型如图所示，A为厚壁玻璃广口瓶，瓶的容积是V0，B为软木塞，C为排水管，D为进气细管，正为圆柱形盛水容器．当
瓶中空气的体积为V1时，潜水艇模型可以停在液面下任何深处，若通过细管D向瓶中压入空气，潜水艇模型上浮，当瓶中空气的体积为2 Vl时，潜水艇模型恰好有一半的体积露出水面，水的密度为恰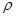
水 ，软木塞B，细管C、D的体积和重以及瓶中的空气重都不计．
求：（1）潜水艇模型的体积；
（2）广口瓶玻璃的密度．
如图所示是甲、乙两种物质的质量和体积的关系图象．若用质量相等的甲、乙两种物质分别制成实心正方体A、B，把它们平放在水平地面上，则两正方体A、B对水平地面的压强之比为：（ ）
A．8︰1 B．4︰3 C．1︰2 D．4︰1
己知铝的密度为2.7×103kg/m3，小明的父亲外出时买了一个用铝材料制造的艺术品球，用天平测得球的质量是594g，体积为300cm3．请你帮助完成下列问题：
（1）判断此球是否为实心的．
（2）若是空心的，则空心部分的体积为多少cm3？
（3）若在空心部分注满水，则注入水的质量为多少？
将一钢球放入盛有100mL水的量筒中，水面上升到150mL处。又用天平称出该球质量为237g。（ρ钢=7．9×l03kg／m3，ρ煤油=0．8×l03kg／m3）求：
（1）此钢球是空心的还是实心的？
（2）若为空心的，空心部分体积是多少？
（3）在空心部分注满煤油，那么钢球的总质量为多少？
“马踏飞燕”是汉代艺术家高度智慧、丰富想象、浪漫主义精神和高超艺术的结晶．飞奔的骏马之所以能用一只蹄稳稳地踏在飞燕上，是因为马的 位置的竖直线能通过飞燕．有一“马踏飞燕”工艺品采用密度为8.0×103 kg/m3的合金材料制造．总体积为1 dm3，飞燕与水平桌面的接触面积为20cm2，则该工艺品的质量为 kg，对水平桌面的压强为 Pa．
甲、乙两种物质的质量和体积关系如图所示，如分别用甲、乙两种物质制成体积相等的两实心物体a和b，放在水中静止后，则
| A．a漂浮，a受浮力大于b | B．b漂浮，b受浮力大于a |
| C．a沉底，a受浮力大于b | D．b沉底，b受浮力大于a |
粤公网安备 44130202000953号