初中数学填空题

将105表示成不少于两个连续的(非零)自然数之和，最多有种表达方式。

如右图所示，ABCD是一个正方形，其中几块阴影部分的面积如图所示，则四边形BMQN的面积为。

如果正整数n使得++++=69，则n为。 (其中[x]表示不超过x的最大整数)

如右图，在10´10的方格中有一个四边形，4个顶点在方格的格点上。如果每个方格的面积为1，则四边形的面积是 。

在下面的加法竖式中，如果不同的汉字代表不同的数字。使得算式成立，那么四位数
“华杯初赛”的最小值是。

下列四个命题:
①一组对边相等且一组对角相等的四边形是平行四边形; ②一组对边相等且一条对角线平分另一条对角线的四边形是平行四边形;③一组对角相等且这一组对角的顶点所联结的对角线被另一条对角线平分的四边形是平行四边形;
④一组对角相等且这一组对角的顶点所联结的对角线平分另一条对角线的四边形是平行四边形.
其中，正确命题的序号是.

AD、BE、CF为△ABC的内角平分线.若BD+BF=CD+CE=AE+AF，则∠BAC的度数为 .

把1，2，…，2 008个正整数分成1 004组:a₁，b₁;a₂，b₂;…;a_{1 004}，b_{1 004}，且满足a₁+b₁=a₂+b₂=…=a₁₀₀₄+b₁₀₀₄.对于所有的i(i=1，2，…，1 004)，a_ib_i的最大值为.

已知方程x²+x-1=0的两个根为α、β.则的值为.

从1， 2，…， 2 006中，至少要取出个奇数，才能保证其中必定存在两个数，它们的和为2 008.

如图，在以O为圆心的两个同心圆图2中，MN为大圆的直径，交小圆于点P、Q，大圆的弦MC交小圆于点A、B.若OM=2，OP= 1，MA=AB=BC，则△MBQ的面积为.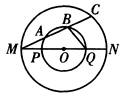

设a、b、c为整数，且对一切实数x，(x-a)(x-8)+1="(x-b)(x-c)" 恒成立.则a+b+c的值为.

正方形ABCD的边长为5，E为边BC上一点，使得BE=3，P是对角线BD上的一点，使得PE+PC的值最小.则PB=.

若，则---，；

如图，在中，，，，动点从点开始沿边向以的速度移动（不与点重合），动点从点开始沿边向以的速度移动（不与点重合）．如果、分别从、同时出发，那么经过_____________秒，四边形的面积最小．