如图.等边△ABC中,∠ABC与∠ACB的平分线相交于点O,且OD∥AB,OE∥AC.
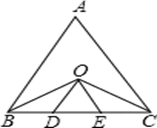
(1)试判定△ODE的形状.并说明你的理由;
(2)线段BD、DE、EC三者有什么关系?写出你的判断过程.
如图,已知△ABC的三个顶点分别为A(2,3)、B(3,1)、C(-2,-2).
(1)请在图中作出△ABC关于y轴对称图形△DEF
(2)写出D、E、F的坐标。
已知如图(1):△ABC中,AB=AC,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.
(1)写出线段EF与BE、CF间的数量关系?(不证明)
(2)若AB≠AC,其他条件不变,如图(2),图中线段EF与BE、CF间是否存在(1)中数量关系?请说明理由.
(3)若△ABC中,AB≠AC,∠B的平分线与三角形外角∠ACD的平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F,如图(3),这时图中线段EF与BE,CF间存在什么数量关系?请说明理由.
雨伞的中截面如图所示,伞骨AB=AC,支撑杆OE=OF,AE= AB,AF=
AB,AF= AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
AC,当O沿AD滑动时,雨伞开闭,问雨伞开闭过程中,∠BAD与∠CAD有何关系?说明理由.
用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形,请你试一试,把拼成的四边形分别画在图3、图4的虚框内。
某校政教处倡导“光盘行动”,让同学们珍惜粮食,但发现还是有少数同学们就餐时剩余饭菜较多,为了让同学们理解这次活动的重要性,政教处在某天午餐中,分别按照七、八、九三个年级总人数的同样比例随机调查了三个年级部分同学这餐饭菜的剩余情况,分为三类:A(没有剩余)、B(有少量剩余)、C(剩余一半及以上),并将结果统计后绘制成了如图所示的不完整的统计图.

(1)这次被调查的同学共有名;
(2)八年级被调查的学生共有名;
(3)通过数据分析,估计这次被调查的所有学生一餐浪费的食物可以供8人用一餐.据此估算,该校1000名学生这餐饭菜没有浪费的学生有多少人?这餐浪费的食物可供多少人食用一餐?