阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,给出它们平行的定义:设一次函数 的图象为直线
的图象为直线 ,一次函数
,一次函数 的图象为直线
的图象为直线 ,若
,若 ,且
,且 ,我们就称直线
,我们就称直线 与直线
与直线 互相平行.已知一次函数
互相平行.已知一次函数 的图象为直线
的图象为直线 ,过点
,过点 且与已知直线
且与已知直线 平行的直线为
平行的直线为 。
。
解答下面的问题:
(1)求 的函数表达式;
的函数表达式;
(2)设直线 分别与
分别与 轴、
轴、 轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求
轴交于点A、B,过坐标原点O作OC⊥AB,垂足为C,求 和
和 两平行线之间的距离 ;
两平行线之间的距离 ;
(3)若Q为OA上一动点,求QP+QB的最小值,并求取得最小值时Q点的坐标。
(4)在 轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
轴上找一点M,使△BMP为等腰三角形,求M的坐标。(直接写出答案)
在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点.
(1)直接写出线段OB的长;
(2)将△OAB绕点O沿逆时针方向旋转90°得到△OA′B′。请你画出△OA′B′,并求在旋转过程中,点B所经过的路径弧BB′的长度.
△ABC在平面直角坐标系xOy中的位置如图所示.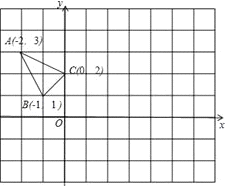
(1)作△ABC关于y轴成轴对称的△A1B1C1;
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2;则此三角形的面积为 .
(3)在x轴上求作一点P,使PA1+PC2的值最小,点P的坐标为 .
如图,在ΔABC与ΔDCB 中,AC与BD 交于点E,且,∠A=∠D,AB=DC.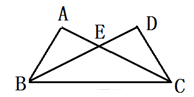
(1)求证:ΔABE≌ΔDCE
(2)当∠AEB=70°时,求∠EBC的度数.
如图,已知∠B=∠C,AD=AE,则AB=AC,请说明理由(填空)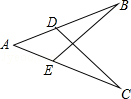
解:在△ABC和△ACD中,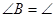 ( )
( )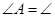 ( )
( )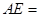 (已知)
(已知)
∴△ABE≌△ACD ( )
∴AB=AC( )
如图,已知反比例函数y=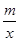 的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).
的图象与一次函数y=ax+b的图象相交于点A(1,4)和点B(n,-2).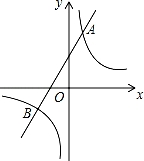
(1)求反比例函数和一次函数的解析式;
(2)当一次函数的值小于反比例函数的值时,直接写出x的取值范围.