初中数学四种命题及其关系选择题

如图，在平面直角坐标系中，四边形OABC是菱形，点C的坐标为（4,0），∠AOC= 60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度向右平移，设直线l与菱形OABC的两边分别交于点M，N（点M在点N的上方），若△OMN的面积为S，直线l的运动时间为t 秒（0≤t≤4）,
则能大致反映S与t的函数关系的图象是（   ）

如下图，动点P从点A出发，沿线段AB运动至点B后，立即按原路返回，点P在运动过程中速度大小不变，则以点A为圆心，线段AP长为半径的圆的面积S与点P的运动时间t之间的函数图像大致为 （      ）

下列函数中，当x＜0时，函数值y随x的增大而增大的有【   】
①y=x    ②y=－2x＋1         ③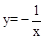       ④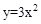

A．1个

B．2个

C．3个

D．4个

若m、n（m<n）是关于x的方程的两根，且a < b，则a、b、m、n 的大小关系是（　 　）

A．m < a < b< n	B．a < m < n < b
C．a < m < b< n	D．m < a < n < b

时钟在正常运行时，时针和分针的夹角会随着时间的变换而变化，设时针与分针的夹角为y度，运行时间为t分，当时间从3：00开始到3：30止，图中能大致表示y与t之间的函数关系的图象是【   】

如图，已知：正方形ABCD边长为1，E、F、G、H分别为各边上的点， 且AE="BF=CG=DH," 设小正方形EFGH的面积为，AE为，则关于的函数图象大致是（    ）

二次函数的图像如图所示，反比列函数与正比列函数在同一坐标系内的大致图像是

某人骑车沿直线旅行，先前进了千米，休息了一段时间，又原路原速返回了千米（），再掉头沿原方向加速行驶，则此人离起点的距离与时间的函数关系的
大致图象是

函数的图象如图所示，下列对该函数性质的论述正确的是

A．该函数的图象是轴对称图形

B．在每个象限内，的值随值的增大而减小

C．当时，该函数在时取得最小值2

D．的值可能为1

在平面直角坐标系中,函数与的图象大致是

为加快把万州建成重庆市第二大都市，天城入城大道加紧施工。该工程全长6.1公里，路面铺设基本完成，目前已进入边坡治理及附属管道安装阶段。若其中某段工程共长1500米，在第6天工程完成一半时，因下雨停工两天，第三天恢复后加快了进度，工作效率是原来的倍，正好按期完工。若用横轴表示工期，纵轴表示未完成的工程量，下面能反映这段工程的图像是(      ).

如图，菱形ABCD中，∠A＝60⁰，AB＝2，动点P从点B出发，以每秒1个单位长度的速度沿B→C→D向终点D运动．同时动点Q从点A出发，以相同的速度沿A→D→B向终点B运动，运动的时间为秒，当点P到达点D时，点P、Q同时停止运动，设△APQ的面积为，则反映与的函数关系的图象是(      )

如图，为圆O的四等分点，动点从圆心出发，沿路线作匀速运动，设运动时间为（t）．，则下列图象中表示与t之间函数关系最恰当的是（     ）

小翔在如图1所示的场地上匀速跑步，他从点A出发，沿箭头所示方向经过点B跑到点C，共用时30秒．他的教练选择了一个固定的位置观察小翔的跑步过程．设小翔跑步的时间为t（单位：秒），他与教练的距离为y（单位：米），表示y与t的函数关系的图象大致如图2所示，则这个固定位置可能是图1中的【   】

A．点M

B．点N

C．点P

D．点Q

小英早上从家里骑车上学，途中想到社会实践调查资料忘带了，立刻原路返回，返家途中遇到给她送资料的妈妈，接过资料后，小英加速向学校赶去．能反映她离家距离s与骑车时间t的函数关系图象大致是