初中数学圆幂定理解答题

如图，在坐标系xOy中，已知D（﹣5，4），B（﹣3，0），过D点分别作DA、DC垂直于x轴，y轴，垂足分别为A、C两点，动点P从O点出发，沿x轴以每秒1个单位长度的速度向右运动，运动时间为t秒．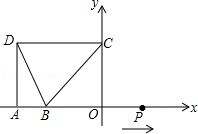

（1）当t为何值时，PC∥DB；
（2）当t为何值时，PC⊥BC；
（3）以点P为圆心，PO的长为半径的⊙P随点P的运动而变化，当⊙P与△BCD的边（或边所在的直线）相切时，求t的值．

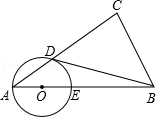
如图，在△ABC中，∠C=90°，AC+BC=9，点O是斜边AB上一点，以O为圆心2为半径的圆分别与AC、BC相切于点D、E。

（1）求AC、BC的长；
（2）若AC=3，连接BD，求图中阴影部分的面积（取3.14）。

如图，在平面直角坐标系中，已知A（8，0），B（0，6），⊙M经过原点O及点A、B．

（1）求⊙M的半径及圆心M的坐标；
（2）过点B作⊙M的切线l，求直线l的解析式；
（3）∠BOA的平分线交AB于点N，交⊙M于点E，求点N的坐标和线段OE的长．

如图，在平面直角坐标系xOy中，一动直线l从y轴出发，以每秒1个单位长度的速度沿x轴向右平移，直线l与直线y=x相交于点P，以OP为半径的⊙P与x轴正半轴交于点A，与y轴正半轴交于点B．设直线l的运动时间为t秒．

（1）填空：当t=1时，⊙P的半径为       ，OA=       ，OB=       ；
（2）若点C是坐标平面内一点，且以点O、P、C、B为顶点的四边形为平行四边形．
①请你直接写出所有符合条件的点C的坐标；（用含t的代数式表示）
②当点C在直线y=x上方时，过A、B、C三点的⊙Q与y轴的另一个交点为点D，连接DC、DA，试判断△DAC的形状，并说明理由．

如图①，AB是半圆O的直径，以OA为直径作半圆C，P是半圆C上的一个动点（P与点A，O不重合），AP的延长线交半圆O于点D，其中OA=4．

（1）判断线段AP与PD的大小关系，并说明理由；
（2）连接OD，当OD与半圆C相切时，求的长；
（3）过点D作DE⊥AB，垂足为E（如图②），设AP=x，OE=y，求y与x之间的函数关系式，并写出x的取值范围．

（1）问题探究
数学课上，李老师给出以下命题，要求加以证明．
如图1，在△ABC中，M为BC的中点，且MA=BC，求证∠BAC=90°．
同学们经过思考、讨论、交流，得到以下证明思路：
思路一 直接利用等腰三角形性质和三角形内角和定理…
思路二 延长AM到D使DM=MA，连接DB，DC，利用矩形的知识…
思路三 以BC为直径作圆，利用圆的知识…
思路四…
请选择一种方法写出完整的证明过程；
（2）结论应用
李老师要求同学们很好地理解（1）中命题的条件和结论，并直接运用（1）命题的结论完成以下两道题：
①如图2，线段AB经过圆心O，交⊙O于点A，C，点D在⊙O上，且∠DAB=30°，OA=a，OB=2a，求证：直线BD是⊙O的切线；
②如图3，△ABC中，M为BC的中点，BD⊥AC于D，E在AB边上，且EM=DM，连接DE，CE，如果∠A=60°，请求出△ADE与△ABC面积的比值．

如图，在⊙C的内接△AOB中，AB=AO=4，tan∠AOB=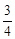，抛物线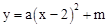（a≠0）经过点A（4，0）与点（﹣2，6）．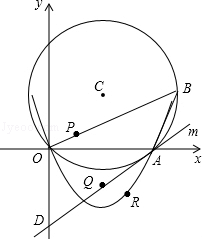

（1）求抛物线的解析式；
（2）直线m与⊙C相切于点A，交y轴于点D，动点P在线段OB上，从点O出发向点B运动，同时动点Q在线段DA上，从点D出发向点A运动，点P的速度为每秒1个单位长，点Q的速度为每秒2个单位长．当PQ⊥AD时，求运动时间t的值．

如图，直线分别与x、y轴交于点B、C，点A（﹣2，0），P是直线BC上的动点．

（1）求∠ABC的大小；
（2）求点P的坐标，使∠APO=30°；
（3）在坐标平面内，平移直线BC，试探索：当BC在不同位置时，使∠APO=30°的点P的个数是否保持不变？若不变，指出点P的个数有几个？若改变，指出点P的个数情况，并简要说明理由．

如图1，△ABC中，CA=CB，点O在高CH上，OD⊥CA于点D，OE⊥CB于点E，以O为圆心，OD为半径作⊙O．

（1）求证：⊙O与CB相切于点E；
（2）如图2，若⊙O过点H，且AC=5，AB=6，连接EH，求△BHE的面积和tan∠BHE的值．

如图1，正方形ABCD的边长为2，点M是BC的中点，P是线段MC上的一个动点（不与M、C重合），以AB为直径作⊙O，过点P作⊙O的切线，交AD于点F，切点为E．

（1）求证：OF∥BE；
（2）设BP=x，AF=y，求y关于x的函数解析式，并写出自变量x的取值范围；
（3）延长DC、FP交于点G，连接OE并延长交直线DC与H（图2），问是否存在点P，使△EFO∽△EHG（E、F、O与E、H、G为对应点）？如果存在，试求（2）中x和y的值；如果不存在，请说明理由．

如图，⊙O的半径为1，直线CD经过圆心O，交⊙O于C、D两点，直径AB⊥CD，点M是直线CD上异于点C、O、D的一个动点，AM所在的直线交于⊙O于点N，点P是直线CD上另一点，且PM=PN．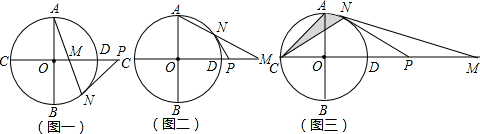

（1）当点M在⊙O内部，如图一，试判断PN与⊙O的关系，并写出证明过程；
（2）当点M在⊙O外部，如图二，其它条件不变时，（1）的结论是否还成立？请说明理由；
（3）当点M在⊙O外部，如图三，∠AMO=15°，求图中阴影部分的面积．

如图，在△ABC中，∠ABC=90°，边AC的垂直平分线交BC于点D，交AC于点E，连接BE．

（1）若∠C=30°，求证：BE是△DEC外接圆的切线；
（2）若BE=，BD=1，求△DEC外接圆的直径．

如图，△ABC内接于⊙O，AB是⊙O的直径，∠BAC=2∠B，⊙O的切线AP与OC的延长线相交于点P。若，求AC的长。

在Rt△ACB中，∠C=90°，点O在AB上，以O为圆心，OA长为半径的圆与AC，AB分别交与点D，E，且∠CBD=∠A．
（1）判断直线BD与⊙O的位置关系，并证明你的结论．
（2）若AD：AO=6：5，BC=3，求BD的长．

已知，如图1，△ABC中，BA=BC，D是平面内不与A、B、C重合的任意一点，∠ABC=∠DBE，BD=BE。
 
（1）求证：△ABD≌△CBE；
（2）如图2，当点D是△ABC的外接圆圆心时，请判断四边形BDCE的形状，并证明你的结论。