△ABC中,∠C=Rt∠,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点E、D,则AE的长为()
A.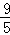 B.
B.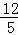 C.
C. D.
D.
如图,等圆⊙O1和⊙O2相交于A、B两点,⊙O1经过⊙O2的圆心O2,连接AO1并延长交⊙O1于点C,则∠ACO2的度数为()
A.60° B.45° C.30° D.20°
如图,已知⊙O的半径为R,C、D是直径AB的同侧圆周上的两点, 的度数为100°,
的度数为100°, =2
=2 ,动点P在线段AB上,则PC+PD的最小值为()
,动点P在线段AB上,则PC+PD的最小值为()
A.RB. RC.
RC.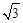 RD.
RD.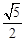 R
R
绍兴是著名的桥乡,如图,圆拱桥的拱顶到水面的距离CD为8m,桥拱半径OC为5m,则水面宽AB为()
| A.4m | B.5m | C.6m | D.8m |
若⊙O的直径为20cm,点O到直线l的距离为10cm,则直线l与⊙O的位置关系是()
| A.相交 | B.相切 | C.相离 | D.无法确定 |
如图,AB、AC是⊙O的两条切线,B、C是切点,若∠A = 70°,则∠BOC的度数为()
A.100° B.110° C.120° D.130°
⊙A半径为5,圆心A的坐标为(1,0),点P的坐标为(-2,4),则点P与⊙A的位置关系是()
| A.点P在⊙A上 | B.点P在⊙A内 |
| C.点P在⊙A外 | D.点P在⊙A上或外 |
如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为()
A.2 B.2
B.2 C.2
C.2 D.8
D.8
如图6,AB是⊙O的直径,AB=8,点M在⊙O上,∠MAB=20°,N是弧MB的中点,P是直径AB上的一动点,若MN=1,则△PMN周长的最小值为().
| A.4 | B.5 | C.6 | D.7 |
如图,已知∠ACB是⊙O的圆周角,∠ACB=50°,则圆心角∠AOB是 ()
| A.40° | B.50° | C.80° | D.100° |
在长方形ABCD中AB=16,如图所示裁出一扇形ABE,将扇形围成一个圆锥(AB和AE重合),则此圆锥的底面半径为()
| A.4 | B.16 | C.4 |
D.8 |