初中数学圆幂定理选择题

如图，正六边形A₁B₁C₁D₁E₁F₁的边长为2，正六边形A₂B₂C₂D₂E₂F₂的外接圆与正六边形A₁B₁C₁D₁E₁F₁的各边相切，正六边形A₃B₃C₃D₃E₃F₃的外接圆与正六边形A₂B₂C₂D₂E₂F₂的各边相切，…按这样的规律进行下去，A₁₀B₁₀C₁₀D₁₀E₁₀F₁₀的边长为（）

A．

B．

C．

D．

如图，△OAB中，OA=OB，∠A=30°，⊙O与AB相切，切点为E，并分别交OA，OB于C，D两点，连接CD.若CD等于，则扇形OCED的面积等于（）.

A．π　 B．πC．πD．π

如图，扇形的半径为1，，以为直径画半圆．则图中阴影部分的面积为（）

A．

B．

C．

D．

如图，C为⊙O直径AB上一动点，过点C的直线交⊙O于D、E两点，且∠ACD=45°，DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时，设AF=，DE=，下列中图象中，能表示与的函数关系式的图象大致是（）

如右图是一个正八边形，图中空白部分的面积等于20，则阴影部分的面积等于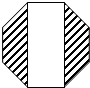

A．20

B．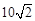

C．18

D．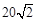

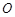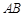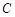如图，以为圆心的两个同心圆中，大圆的弦切小圆于点，若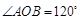，则大圆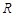半径与小圆半径之间满足（）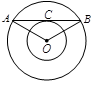

A．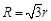

B．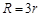

C．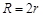

D．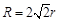

一个点到圆上的最小距离是4，最大距离是9，则圆的半径是（）

A．2．5

B．2．5或6．5

C．6．5

D．5或13

如图，在△ABC中，AB=10，AC=8，BC=6，经过点C且与边AB相切的动圆与CB，CA分别相交于点E，F，则线段EF长度的最小值是（）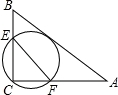

A．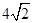

B．4.75

C．5

D．4.8

⊙A半径为5，圆心A的坐标为（1，0），点P的坐标为（-2，4），则点P与⊙A的位置关系是（）

A．点P在⊙A上	B．点P在⊙A内
C．点P在⊙A外	D．点P在⊙A上或外

如图，在平面直角坐标系中，点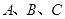的坐标为（1，4）、（5，4）、（1、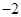），则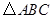外接圆的圆心坐标是（）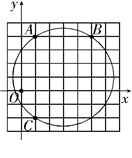

A．（3，1）

B．（3，2）

C．（1，3）

D．（2，3）

如图，在Rt△ABC中∠ACB=90°，AC=6，AB=10，CD是斜边AB上的中线，以AC为直径作⊙O，设线段CD的中点为P，则点P与⊙O的位置关系是（）

A．点P在⊙O内	B．点P在⊙O上
C．点P在⊙O外	D．无法确定

如图，BC是O的直径，P是CB延长线上的一点，PA切O于点A，如果PA＝，PB＝1，
那么∠APC等于（）

A．15°

B．30°

C．45°

D．60°

若⊙O的半径为5cm，点A到圆心O的距离为4cm，那么点A与⊙O的位置关系是（）

A．点A在圆外

B．点A在圆上

C．点A在圆内

D．不能确定

如图，AB为⊙O直径，弦CD⊥AB于点E，已知CD=12，BE=2，则⊙O的直径为：

A．8

B．10

C．16

D．20

如图，在边长为1的正方形组成的网格中，△ABC的顶点都在格点上，将△ABC绕点C顺时针旋转60°，则顶点A所经过的路径长为(　　)

A．10π	B．
C．π	D．π