在平面直角坐标系 中,点M(
中,点M( ,
, ),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与x轴、y轴的另一交点分别为点D,A(如图),连接AM点P是弧AB上的动点.
),以点M为圆心,OM长为半径作⊙M ,使⊙M与直线OM的另一交点为点B,与x轴、y轴的另一交点分别为点D,A(如图),连接AM点P是弧AB上的动点.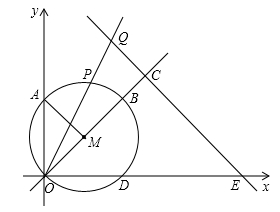
(1)写出∠AMB的度数;
(2)点Q在射线OP上,且OP·OQ=20,过点Q作QC垂直于直线OM,垂足为C,直线QC交x轴于点E.
①当动点P与点B重合时,求点E的坐标;
②连接QD,设点Q的纵坐标为t,△QOD的面积为S,求S与t的函数关系式及S的取值范围.
如图,在平面直角坐标系中,直线y= x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M与x轴、直线AB都相切,其半径为3(1﹣
x+1分别与两坐标轴交于B,A两点,C为该直线上的一动点,以每秒1个单位长度的速度从点A开始沿直线BA向上移动,作等边△CDE,点D和点E都在x轴上,以点C为顶点的抛物线y=a(x﹣m)2+n经过点E.⊙M与x轴、直线AB都相切,其半径为3(1﹣ )a.
)a.
(1)求点A的坐标和∠ABO的度数;
(2)当点C与点A重合时,求a的值;
(3)点C移动多少秒时,等边△CDE的边CE第一次与⊙M相切?
在平面直角坐标系 中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作
中,对于⊙A上一点B及⊙A外一点P,给出如下定义:若直线PB与 x轴有公共点(记作M),则称直线PB为⊙A的“x关联直线”,记作 .
.
(1)已知⊙O是以原点为圆心,1为半径的圆,点P(0,2),
①直线 :
: ,直线
,直线 :
: ,直线
,直线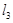 :
: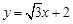 ,直线
,直线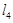 :
: 都经过点P,在直线
都经过点P,在直线 ,
,  ,
, 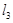 ,
, 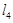 中,是⊙O的“x关联直线”的是;
中,是⊙O的“x关联直线”的是;
②若直线 是⊙O的“x关联直线”,则点M的横坐标
是⊙O的“x关联直线”,则点M的横坐标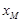 的最大值是;
的最大值是;
(2)点A(2,0),⊙A的半径为1,
①若P(-1,2),⊙A的“x关联直线” :
: ,点M的横坐标为
,点M的横坐标为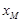 ,当
,当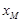 最大时,求k的值;
最大时,求k的值;
②若P是y轴上一个动点,且点P的纵坐标 ,⊙A的两条“x关联直线”
,⊙A的两条“x关联直线” ,
,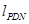 是⊙A的两条切线,切点分别为C,D,作直线CD与x轴点于点E,当点P的位置发生变化时, AE的长度是否发生改变?并说明理由.
是⊙A的两条切线,切点分别为C,D,作直线CD与x轴点于点E,当点P的位置发生变化时, AE的长度是否发生改变?并说明理由.
如图,在△ABC中,∠ABC=∠ACB,以AC为直径的⊙O分别交AB、BC于点M、N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线.
(2)若BC=2 ,sin∠BCP=
,sin∠BCP= ,求点B到AC的距离.
,求点B到AC的距离.
(3)在第(2)的条件下,求△ACP的周长.
如图,等边△ABC的周长为6π,半径是1的⊙O从与AB相切于点D的位置出发,在△ABC外部按顺时针方向沿三角形滚动,又回到与AB相切于点D的位置,则⊙O自转了( )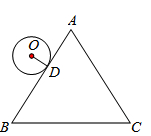
| A.2周 | B.3周 | C.4周 | D.5周 |
如图1,在第一象限内,直线 与过点
与过点 且平行于
且平行于 轴的直线
轴的直线 相交于点
相交于点 ,半径为
,半径为 的⊙
的⊙ 与直线
与直线 、
、 轴分别相切于点
轴分别相切于点 、
、 ,且与直线
,且与直线 分别交于不同的
分别交于不同的 、
、 两点.
两点.
(1)当点A的坐标为 时,
时,
① 填空: =,
=, =,
=, =;
=;
②如图2,连结
 ,
, 交直线
交直线 于
于 ,当
,当 时,试说明以
时,试说明以 、
、  、
、 、
、 为顶点的四边形是等腰梯形;
为顶点的四边形是等腰梯形;
(2)在图1中,连结 并延长交⊙
并延长交⊙ 于点
于点 ,试探索:对不同的
,试探索:对不同的 取值,经过
取值,经过 、
、 、
、 三点的抛物线
三点的抛物线 ,
, 的值会变化吗?若不变,求出
的值会变化吗?若不变,求出 的值;若变化,请说明理由.
的值;若变化,请说明理由.
如图,PA、PB切⊙O于A、B两点,CD切⊙O于点E,交PA,PB于C、D,若⊙O的半径为r,△PCD的周长等于3r,则tan∠APB的值是()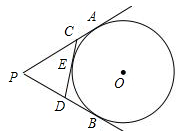
A.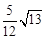 B.
B.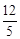 C.
C.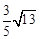 D.
D.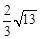
已知“6”字形图中,FM是大⊙O的直径, BC与大⊙O相切于B, OB与小⊙O相交于A, AD∥BC,CD∥BH∥FM, DH⊥BH于H,设∠FOB=30°,OB="4," BC=6.
﹙1﹚求证:AD为小⊙O的切线;
﹙2﹚求DH的长.﹙结果保留根号﹚
如图,在矩形ABCD中,AB=20cm,BC=4cm,点p从A开始折线A——B——C——D以4cm/秒的 速度 移动,点Q从C开始沿CD边以1cm/秒的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动的时间t(秒)
(1)t为何值时,四边形APQD为矩形.
(2)如图(2),如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?
如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.
(1)求证:CF是⊙O的切线;
(2)求证:△ACM∽△DCN;
(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=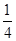 ,求BN的长.
,求BN的长.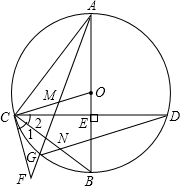
一块△ABC余料,已知AB=8cm,BC=15cm,AC=17cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是 .
如图,AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.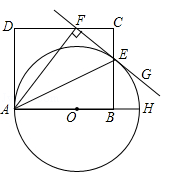
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.
(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径.
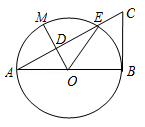
如图,以线段AB为直径的⊙O交线段AC于点E,点D是AE的中点,连接OD并延长交⊙O于点M,∠BOE=60°,cosC=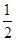 ,BC=
,BC=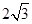 .
.
(1)求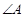 的度数;
的度数;
(2)求证:BC是⊙ 的切线;
的切线;
(3)求弧AM的长度.
如图1,在直角梯形ABCD中,AD∥BC,∠A=90°,BD⊥DC,BC=10cm,CD=6cm.在线段BC、CD上有动点F、E,点F以每秒2cm的速度,在线段BC上从点B向点C匀速运动;同时点E以每秒1cm的速度,在线段CD上从点C向点D匀速运动.当点F到达点C时,点E同时停止运动.设点F运动的时间为t(秒).
(1)求AD的长;
(2)设四边形BFED的面积为y,求y 关于t的函数关系式并写出自变量的取值范围
(3)当t为何的值时,以EE为半径的⊙F与CD边只有一个公共点.