(1)如图1,OA、OB是⊙O的半径,且OA⊥OB,点C是OB延长线上任意一点,过点C作CD切⊙O于点D,连结AD交DC于点E.则CD=CE吗?如成立,试说明理由。
(2)若将图中的半径OB所在直线向上平行移动交OA于F,交⊙O于B’,其他条件不变,如图2,那么上述结论CD=CE还成立吗?为什么?
(3)若将图中的半径OB所在直线向上平行移动到⊙O外的CF,点E是DA的延长线与CF的交点,其他条件不变,如图3,那么上述结论CD=CE还成立吗?为什么
相关知识点
推荐套卷
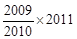
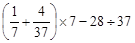
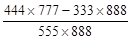
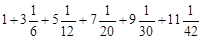
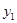 (元)、
(元)、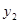 (元),写出
(元),写出
 ,其中
,其中 .
. 粤公网安备 44130202000953号
粤公网安备 44130202000953号