初中数学圆幂定理试题

如图所示，正方形网格中，每个小正方形的边长为1个单位，以O为原点建立平面直角坐标系．圆心为A（3，0）的A被y轴截得的弦长BC＝8．解答下列问题：

（1）⊙A的半径为           ；
（2）若将⊙A先向上平移2个单位，再向右平移3个单位得到⊙D，则⊙D的圆心D点的坐标是           ；⊙D与x轴的位置关系是           ；⊙D与y轴的位置关系是           ；
（3）若将⊙A沿着水平方向平移           个单位长度，⊙A即可与y轴相切．

如图，要拧开一个边长为的正六边形螺帽，扳手张开的开口至少为（   ）

A．

B．

C．

D．

将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上，点A、B的读数分别为86°、30°，则∠ACB的大小为（     ）

A．15°         B．28°       C．29°           D．34°

图中，△ABC外接圆的圆心坐标是     ．

如图，AB是⊙O的直径，CD为⊙O的一条弦，CD⊥AB于点E，已知CD=8，OE=1，则⊙O的半径为          ．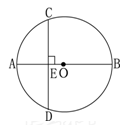

如图，用一个半径为30cm，面积为300πcm²的扇形铁皮，制作一个无底的圆锥（不计损耗），则圆锥的底面半径r为         ．
 

如图，水平放置的圆柱形排水管道的截面直径是1m，其中水面的宽AB为0．8m，则排水管内水的深度为            m．

如图，AB是半圆O直径，半径OC⊥AB，连接AC，∠CAB的平分线AD分别交OC于点E，交于点D，连接CD、OD，以下三个结论：
①AC∥OD；②AC＝2CD；③CD²=CE·CO，其中所有正确结论的序号是（   ）

A．①②      B．①③    C．②③         D．①②③

直角三角形的两条边长分别为6和8，那么这个三角形的外接圆半径等于______．

已知扇形的圆心角为120°，半径为2厘米，则这个扇形的弧长为__________厘米．

如图，在△ABC中，AB＝AC＝10，以AB为直径的⊙O分别交AC、BC于点D、E，点F在AC的延长线上，且∠CBF＝∠A，tan∠CBF＝，则CF的长为

A．          B．             C．       D．

如图，点A（－10，0），B（－6，0），点C在y轴的正半轴上，∠CBO＝45°，CD∥AB，∠CDA＝90°．点P从点Q（8，0）出发，沿x轴向左以每秒1个单位长的速度向点A匀速运动，运动时间为t秒．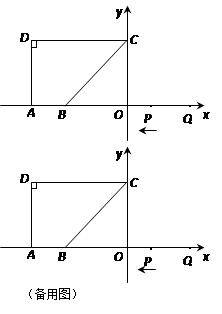

（1）求点C的坐标．
（2）当∠BCP＝15°时，求t的值．
（3）以PC为直径作圆，当该圆与四边形ABCD的边（或边所在的直线）相切时，求t的值．

如图，Rt△ABC中，∠C＝90^o，O为AB上一点，以O为圆心，OB长为半径的圆，交BC边于点D，与AC边相切于点E．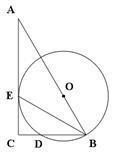

（1）求证：BE平分∠ABC；
（2）若CD︰BD＝1︰2，AC＝4，求CD的长．

如图，AB是⊙O的直径，AC、DC为弦，∠ACD＝60°，P为AB延长线上的点，∠APD＝30°．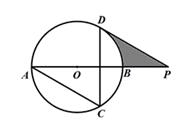

（1）求证：DP是⊙O的切线．
（2）若⊙O的半径为3cm，求图中阴影部分的面积．

△ABC中，∠ACB=120°，AC=BC=3，点D为平面内一点，满足∠ADB=60°，若CD的长度为整数，则所有满足题意的CD的长度的可能值为             ．