初中数学三角形的五心试题

如图所示，在△ABC中，AE、BF是角平分线，它们相交于点O，AD是高，∠BAC=50°，∠C=70°，求∠DAC、∠BOA的度数．

如图，已知:EC=AC，∠BCE=∠DCA，∠A=∠E．求证：∠B=∠D．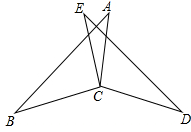

如图，在△ABC中，∠BAC=50°，AD为∠BAC的平分线，DE⊥AB，DF⊥AC，则∠DEF=     ．

一个多边形内角和是一个四边形内角和的4倍，则这个多边形的边数是       ．

若等腰三角形的一个外角为100°，则它的顶角为          ．

如图点A、D、C、E在同一条直线上，AB∥EF，AB=EF，∠B=∠F，AE=10，AC=7，则CD的长为（ ）

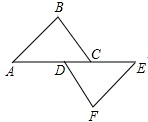
A．5．5              B．4               C．4．5            D．3

把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为（ ）

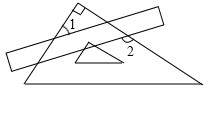
A．120°

B．125°

C．130°

D．140°

等腰三角形的一条边长为6，另一边长为13，则它的周长为（ ）

A．25

B．25或32

C．32

D．19

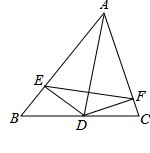
如图，在△ABC中，AB＝BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD＝45°，AD与BE交于点F，连接CF．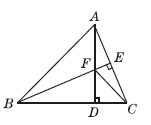

（1）求证：BF＝2AE；
（2）若CD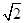＝，求AD的长．

探索与研究：
方法1：如图（a），对任意的符合条件的直角三角形绕其锐角顶点旋转90°所得，所以
∠BAE＝90°，且四边形ACFD是一个正方形，它的面积和四边形ABFE面积相等，而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和，根据图示写出证明勾股定理的过程；
方法2：如图（b），是任意的符合条件的两个全等的Rt△BEA和Rt△ACD拼成的，你能根据图示再写一种证明勾股定理的方法吗？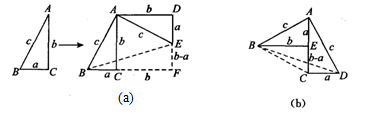

已知，如图，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．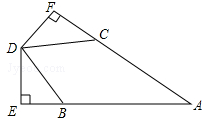

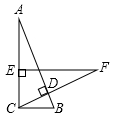
如图，在Rt△ABC中，∠ACB=90°，BC=2cm，CD⊥AB，在AC上取一点E，使EC=BC，过点E作EF⊥AC交CD的延长线于点F，若EF=5cm，则AE=          cm．

已知一个等腰三角形的顶角为100°，则它的底角为___________．

已知一个直角三角形的两条直角边分别为6和8，则它斜边上的中线的长为____  ___．

如图，AD＝AB＝BC，那么∠1和∠2之间的关系是    （  ）

A．∠1＝∠2

B．2∠1+∠2＝180°

C．∠1+3∠2＝180°

D．3∠1－∠2＝180°