初中数学一次函数的最值解答题

直线l经过（2，3）和（-2,-1）两点，它还与x轴交于A点，与y轴交于C点，与经过原点
的直线OB交于第三象限的B点，且∠ABO=30°．求：

（1）点A、C的坐标；
（2）点B的坐标．

小明妈妈，每天需赶头班公交车，驶往终点站．离他家最近的公交站点离终点站15km，一天他妈妈从家步行到公交站点，恰好赶上头班公交车，上车后才发现有重要物品落在家中，急忙通知小明将物品送到终点站，这时妈妈已上车5min，小明马上取了东西，用时6min赶到妈妈上车的公交站点，乘坐刚好路过的出租车，沿公交车的线路驶往公交车的终点站，结果比公交车早4min到达，出租车与小明一起等候公交车．若公交车，出租车均视为全程匀速行驶，出租车的速度为60km/h（即：1km/min）．设妈妈所乘公交车离开她上车的站点的时间为t（min），小明上车后，小明所乘出租车距妈妈上车的公交站点的路程为S₁（km），妈妈所乘的公交车与小明所乘出租车之间相距的路程为S（km）
（1）求S₁与t之间的函数关系式，并写出t的取值范围；
（2）写出11≤t≤30，S与t之间的函数关系式；
（3）公交车到达终点之前，经多长时间两车相距500m．

光明文具厂工人的工作时间：每月26天，每天8小时．待遇：按件计酬，多劳多得，每月另加福利工资920元，按月结算．该厂生产A，B两种型号零件，工人每生产一件A种型号零件，可得报酬0．85元，每生产一件B种型号零件，可得报酬1．5元，下表记录的是工人小王的工作情况：

生产A种型号零件/件	生产B种型号零件/件	总时间/分
2	2	70
6	4	170

 
根据上表提供的信息，请回答如下问题：
（1）小王每生产一件A种型号零件、每生产一件B种型号零件，分别需要多少分钟？
（2）设小王某月生产A种型号零件x件，该月工资为y元，求y与x的函数关系式；
（3）如果生产两种型号零件的数目限制，那么小王该月的工资数目最多为多少？

直线与x轴、y轴分别交于A、B两点，点E从B点出发，以每秒1个单位长度的速度沿线段BO向O点移动（不考虑点E与B、O两点重合的情况），过点E作EF∥AB，交x轴于点F，将四边形ABEF沿直线EF折叠后，与点A对应的点记作点C，与点B对应的点记作点D，得到四边形CDEF，设点E的运动时间为t秒．

（1）画出当t=2时，四边形ABEF沿直线EF折叠后的四边形CDEF（不写画法）；
（2）在点E运动过程中，CD交x轴于点G，交y轴于点H，试探究t为何值时，△CGF的面积为；
（3）设四边形CDEF落在第一象限内的图形面积为S，求S关于t的函数解析式，并求出S的最大值．

某地区为了鼓励市民节约用水，计划实行生活用水按阶梯式水价计费，每月用水量不超过10吨（含10吨）时，每吨按基础价收费；每月用水量超过10吨时，超过的部分每吨按调节价收费．例如，第一个月用水16吨，需交水费17.8元，第二个月用水20吨，需交水费23元．
（1）求每吨水的基础价和调节价；
（2）设每月用水量为n吨，应交水费为m元，写出m与n之间的函数解析式；
（3）若某月用水12吨，应交水费多少元？

某蔬菜经销商去蔬菜生产基地批发某种蔬菜，已知这种蔬菜的批发量在20千克～60千克之间（含20千克和60千克）时，每千克批发价是5元；若超过60千克时，批发的这种蔬菜全部打八折，但批发总金额不得少于300元．
（1）根据题意，填写如表：

（2）经调查，该蔬菜经销商销售该种蔬菜的日销售量y（千克）与零售价x（元/千克）是一次函数关系，其图象如图，求出y与x之间的函数关系式；
（3）若该蔬菜经销商每日销售此种蔬菜不低于75千克，且当日零售价不变，那么零售价定为多少时，该经销商销售此种蔬菜的当日利润最大？最大利润为多少元？

盘锦红海滩景区门票价格80元/人，景区为吸引游客，对门票价格进行动态管理，非节假日打a折，节假日期间，10人以下（包括10人）不打折，10人以上超过10人的部分打b折，设游客为x人，门票费用为y元，非节假日门票费用（元）及节假日门票费用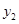（元）与游客x（人）之间的函数关系如图所示．

（1）a=     ，b=     ；
（2）直接写出、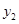与x之间的函数关系式；
（3）导游小王6月10日（非节假日）带A旅游团，6月20日（端午节）带B旅游团到红海滩景区旅游，两团共计50人，两次共付门票费用3040元，求A、B两个旅游团各多少人？

一个批发商销售成本为20元/千克的某产品，根据物价部门规定：该产品每千克售价不得超过90元，在销售过程中发现的售量y（千克）与售价x（元/千克）满足一次函数关系，对应关系如下表：

（1）求y与x的函数关系式；
（2）该批发商若想获得4000元的利润，应将售价定为多少元？
（3）该产品每千克售价为多少元时，批发商获得的利润w（元）最大？此时的最大利润为多少元？

某农场急需铵肥8吨，在该农场南北方向分别有一家化肥公司A、B，A公司有铵肥3吨，每吨售价750元；B公司有铵肥7吨，每吨售价700元，汽车每千米的运输费用b（单位：元/千米）与运输重量a（单位：吨）的关系如图所示．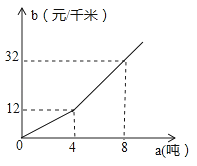

（1）根据图象求出b关于a的函数解析式（包括自变量的取值范围）；
（2）若农场到B公司的路程是农场到A公司路程的2倍，农场到A公司的路程为m千米，设农场从A公司购买x吨铵肥，购买8吨铵肥的总费用为y元（总费用=购买铵肥费用+运输费用），求出y关于x的函数解析式（m为常数），并向农场建议总费用最低的购买方案．

现正是闽北特产杨梅热销的季节，某水果零售商店分两批次从批发市场共购进杨梅40箱，已知第一、二次进货价分别为每箱50元、40元，且第二次比第一次多付款700元．
（1）设第一、二次购进杨梅的箱数分别为a箱、b箱，求a，b的值；
（2）若商店对这40箱杨梅先按每箱60元销售了x箱，其余的按每箱35元全部售完．
①求商店销售完全部杨梅所获利润y（元）与x（箱）之间的函数关系式；
②当x的值至少为多少时，商店才不会亏本．
（注：按整箱出售，利润=销售总收入﹣进货总成本）

如图，一次函数的图象与反比例函数的图象交于A（﹣1，m）、B（n，﹣1）两点．

（1）求一次函数的解析式；
（2）求△AOB的面积．

某工厂生产一种产品，当产量至少为10吨，但不超过55吨时，每吨的成本（万元/吨）与产量（吨）之间是一次函数关系，函数与自变量的部分对应值如下表：

（吨）	10	20	30
（万元/吨）	45	40	35

 
（1）求与的函数关系式，并写出自变量的取值范围；
（2）当投入生产这种产品的总成本为1200万元时，求该产品的总产量；（注：总成本=每吨成本×总产量）
（3）市场调查发现，这种产品每月销售量（吨）与销售单价（万元/吨）之间满足如图所示的函数关系．该厂第一个月按同一销售单价卖出这种产品25吨，请求出该厂第一个月销售这种产品获得的利润．（注：利润=售价—成本）

小慧和小聪沿图1中的景区公路游览．小慧乘坐车速为30km/h的电动汽车，早上7：00从宾馆出发，游玩后中午12：00回到宾馆．小聪骑车从飞瀑出发前往宾馆，速度为20km/h，途中遇见小慧时，小慧恰好游完一景点后乘车前往下一景点．上午10：00小聪到达宾馆．图2中的图象分别表示两人离宾馆的路程s（km）与时间t（h）的函数关系．试结合图中信息回答：

（1）小聪上午几点钟从飞瀑出发？
（2）试求线段AB、GH的交点B的坐标，并说明它的实际意义．
（3）如果小聪到达宾馆后，立即以30km/h的速度按原路返回，那么返回途中他几点钟遇见小慧？

甲、乙两车从A地出发沿同一路线驶向B地，甲车先出发匀速驶向B地．40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B地．甲乙两车距A地的路程y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示．
请结合图象信息解答下列问题：

（1）直接写出a的值，并求甲车的速度；
（2）求图中线段EF所表示的y与x的函数关系式，并直接写出自变量x的取值范围；
（3）乙车出发多少小时与甲车相距15千米？直接写出答案．

如图，已知反比例函数与一次函数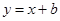的图象在第一象限相交于点A（1，﹣k+4）．

（1）试确定这两个函数的表达式；
（2）求出这两个函数图象的另一个交点B的坐标，并求△AOB的面积．