甲、乙两同学骑自行车从A地沿同一条路到B地，已知乙比甲先出发，他们离出发地的距离s（km）和骑行时间t（h）之间的函数关系如图所示，给出下列说法：
（1）他们都骑行了20km；
（2）乙在途中停留了0．5h；
（3）甲、乙两人同时到达目的地；
（4）相遇后，甲的速度小于乙的速度．
根据图象信息，以上说法正确的有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
如图，函数y=2x和y=ax+4的图象相交于点A（m，3），则不等式2x≤ax+4的解集为（ ）
A． |
B．x≥3 | C． |
D．x≤3 |
一次函数y=2x﹣4的图象与两坐标轴交点的距离是（ ）
A． |
B． |
C． |
D． |
反比例函数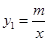
（
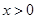）的图象与一次函数
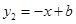的图象交于A，B两点，其中A（1，2），当
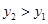时，x的取值范围是（ ）
| A．x＜1 | B．1＜x＜2 | C．x＞2 | D．x＜1或x＞2 |
一辆自行车在公路上行驶，中途发生了故障，停下修理一段时间后继续前进．已知行驶路程S（千米）与所用时间t（时）的函数关系的图象如图所示，那么自行车发生故障后继续前进的速度为（ ）
| A．20千米/时 | B． 千米/时 |
| C．10千米/时 | D． 千米/时 |
小李与小陆从A地出发，骑自行车沿同一条路行驶到B地，他们离出发地的距离S（单位：km）和行驶时间t（单位：h）之间的函数关系的图象如图所示，根据图中提供的信息，有下列说法：
（1）他们都行驶了20km；
（2）小陆全程共用了1．5h；
（3）小李与小陆相遇后，小李的速度小于小陆的速度；
（4）小李在途中停留了0．5h．
其中正确的有（ ）
| A．4个 | B．3个 | C．2个 | D．1个 |
正比例函数y=kx（k≠0）的函数值y随x的增大而增大，则一次函数y=x+k的图象大致是（ ）
如图，边长分别为1和2的两个等边三角形，开始它们在左边重合，大三角形固定不动，然后把小三角形自左向右平移直至移出大三角形外停止．设小三角形移动的距离为x，两个三角形重叠面积为y，则y关于x的函数图象是（ ）
已知点M（1，a）和点N（2，b）是一次函数y=-2x+1图象上的两点，则a与b的大小关系是（ ）
| A．a＞b | B．a=b | C．a＜b | D．以上都不对 |
如图，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是A→D→C→B→A，设P点经过的路线为
，以点A、P、D为顶点的三角形的面积是
．则下列图象能大致反映与的函数关系的是（ ）．
直线
的图象经过第（ ）象限
| A．二、三、四 | B．一、二、四 | C．一、三、四 | D．一、二、三 |
如图，直线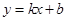
与y轴交于点（0，3）、与x轴交于点（a，0），当a满足
时，k的取值范围是（ ）
A． |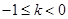
B． |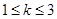
C． |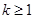
D． |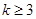
均匀地向如图的容器中注满水，能反映在注水过程中水面高度h随时间t变化的函数图象是（ ）
A． |
B． |
C． |
D． |
下列命题：①对角线互相垂直的四边形是菱形；
②点G是△ABC的重心，若中线AD=6，则AG=3；
③若直线
经过第一、二、四象限，则k＜0，b＞0；
④定义新运算：a*b=
，若（2x）*（x﹣3）=0，则x=1或9；
⑤抛物线
的顶点坐标是（1，1）．
其中是真命题的有 （只填序号）
粤公网安备 44130202000953号
向上平移
个单位后，与直线
的交点在第一象限，则