下列各点中,在函数y=2x-6的图象上的是( )
| A.(-2,3) | B.(3,-2) | C.(1,4) | D.(4,2) |
如图4,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A、B的坐标分别为(1,0)、(4,0),将△ABC沿x轴向右平移,当点C落在直线 上时,线段BC扫过的面积为( )
上时,线段BC扫过的面积为( )
| A.4 | B.8 | C.16 | D. |
用图象法解某二元一次方程组时,在同一直角坐标系中作出相应的两个一次函数的图象如图所示,则所解的二元一次方程组是( )
A. |
B. |
C. |
D. |
下列图形中,表示一次函数 与正比例函数
与正比例函数 (
( 、
、 为常数,且
为常数,且 )的图象的是( )
)的图象的是( )
A. |
B. |
C. |
D. |
在平面直角坐标系中,把直线 向右平移一个单位长度后,其直线解析式为( )
向右平移一个单位长度后,其直线解析式为( )
A. |
B. |
C. |
D. |
某运输公司的一艘轮船在长江上航行,往返于万州、朝天门两地.假设轮船在静水中的速度不变,长江的水流速度不变,该轮船从万州出发,逆水航行到朝天门,停留一段时间(卸货、装货、加燃料等),又顺水航行返回万州.若该轮船从万州出发后所用的时间为x(小时),轮船距万州的距离为y(千米),则下列各图形中,能够反映y与x之间函数关系的大致图象是( )
A. |
B. |
C. |
D. |
如图1,在等腰梯形ABCD中,∠B=60°,PQ同时从B出发,以每秒1单位长度分别沿BADC和BCD方向运动至相遇时停止,设运动时间为t(秒),△BPQ的面积为S(平方单位),S与t的函数图象如图2所示,则下列结论错误的是( )
A.当t=4秒时,S=4 |
| B.AD=4 |
C.当4≤t≤8时,S=2 t t |
| D.当t=9秒时,BP平分梯形ABCD的面积 |
把直线y=-x+3向上平移m个单位后,与直线y=2x+4的交点在第一象限,则m的取值范围是( ).
A. >1 >1 |
B.3< <4 <4 |
C.1< <7 <7 |
D. <4 <4 |
如图,一次函数与反比例函数的图象相交于A、B两点,则图中使反比例函数的值小于一次函数的值的x的取值范围是( )
A.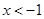 B.
B.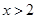
C.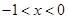 或
或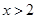 D.
D.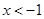 或
或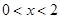
如图,平面直角坐标系中,△ABC的顶点坐标分别是A( 3,1),B( 1,1),C( 2,2),当直线y﹦ x+b与△ABC有公共点时,b的取值范围是( )
x+b与△ABC有公共点时,b的取值范围是( )
A.1≤b≤ |
B.1≤b≤1 | C. ≤b≤1 ≤b≤1 |
D. ≤b≤ ≤b≤ |
如图,直线y=- x+k与y轴交于点A,与双曲线y=
x+k与y轴交于点A,与双曲线y= 在第一象象交于B、C两点,且AB·AC=9,则k=( )
在第一象象交于B、C两点,且AB·AC=9,则k=( )
A. B.
B. C.
C. D.2
D.2
如图,在矩形ABCD中,AB=2,AD=3,点E是BC边上靠近点B的三等分点,动点P从点A出发,沿路径A→D→C→E运动,则△APE的面积y与点P经过的路径长x之间的函数关系用图象表示大致是( )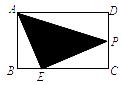

甲、乙两人以相同路线前往距离单位10km的培训中心参加学习.图中l甲、l乙分别表示甲、乙两人前往目的地所走的路程S(km)随时间t变化的函数图象.以下说法:
①乙比甲提前12分钟到达;
②甲的平均速度为15千米/小时;
③乙走了8km后遇到甲;
④乙出发6分钟后追上甲.
其中正确的有( ) 
| A.4个 | B.3个 | C.2个 | D.1个 |
直线 与
与 的交点在第一象限,则
的交点在第一象限,则 的取值可以是( )
的取值可以是( )
| A.-1 | B.0 | C.1 | D.2 |