初中数学一次函数的最值试题

地铁1号线是重庆轨道交通线网东西方向的主干线，也是贯穿渝中区和沙坪坝区的重要交通通道，它的开通极大地方便了市民的出行。现某同学要从沙坪坝到两路口，他先匀速步行至沙坪坝地铁站，等了一会，然后搭乘一号线地铁直达两路口（忽略途中停靠站的时间）。在此过程中，他离沙坪坝的距离的函数关系的大致图象是（    ）

如图，已知直线y=ax+b和直线y=kx交于点P（-4，-2），则关于x，y的二元一次方程组的解是       ．

阅读下面的材料：
在平面几何中，我们学过两条直线平行的定义．下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数的图象为直线，一次函数的图象为直线，若，且，我们就称直线与直线互相平行．已知一次函数的图象为直线，过点且与已知直线平行的直线为。
解答下面的问题：
（1）求的函数表达式；
（2）设直线分别与轴、轴交于点A、B，过坐标原点O作OC⊥AB，垂足为C，求和两平行线之间的距离 ；
（3）若Q为OA上一动点，求QP+QB的最小值，并求取得最小值时Q点的坐标。
（4）在轴上找一点M，使△BMP为等腰三角形，求M的坐标。（直接写出答案）

如图所示的计算程序中，y与x之间的函数关系所对应的图象应为（ ）

A．

B．

C．

D．

写一个y随x的增加而增大的一次函数解析式            ．

已知y与x成正比例，且当x=1时，y=0.5，则y与x的函数关系式是      ．

已知一次函数的图象经过点（m，－8），则m=      ．

正比例函数y=kx（k≠0）的图象在第二、四象限，则一次函数y=x+k的图象大致是 （ ）

A．

B．

C．

D．

如图，求图中直线的函数表达式：

已知正比例函数y=kx（k≠0）的图象经过点（1，-2），则正比例函数的解析式为（ ）

A．y="2x"

B．y="-2x"

C．y=x

D．y=-x

一次函数y=kx+b，当k＞0，b＜0时，它的图象是（ ）

A．

B．

C．

D．

正比例函数y＝kx的图象经过点，则的值是        ．

下列函数：①y=-πx，②y＝-0．125x，③y=8，④y=-8x²+6，⑤y=-0．5x-1中，一次函数有（ ）

A．1个

B．2个

C．3个

D．4个

某机动车出发前油箱内有油42L，行驶若干小时后，途中在加油站加油若干升，油箱中余油量Q（L）与行驶时间t（h）之间的函数关系如图所示，根据图回答问题：

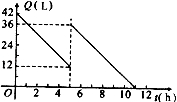
（1）机动车行驶            h后加油；
（2）加油前油箱余油量Q与行驶时间t的函数关系式是            ；
（3）中途加油             L；
（4）如果加油站距目的地还有230km，车速为40km/h，要到达目的地，油箱中的油是否够用？请说明理由．

下列图象中，表示直线的是（     ）

A．

B．

C．

D．