一元二次方程 的解是()
的解是()
| A.x1=1,x2=2 |
B. |
C. |
| D.x1=0,x2=2 |
某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为3万元,可变成本逐年增长,已知该养殖户第1年的可变成本为2.4万元,设可变成本平均每年增长的百分率为x.
(1)用含x的代数式表示第3年的可变成本为 万元.
(2)如果该养殖户第3年的养殖成本为6.456万元,求可变成本平均每年增长的百分率?
某家用电器经过两次降价,每台零售价由1000元下降到810元.若两次降价的百分率相同,则这个百分率为 .
根据下列表格的对应值:
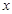 |
0.00 |
0.25 |
0.50 |
0.75 |
1.00 |
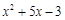 |
-3.00 |
-1.69 |
-0.25 |
1.31 |
3.00 |
可得方程x2+5x-3=0一个解x的范围是()
A.0<x<0.25B.0.25<x<0.50
C.0.50<x<0.75D.0.75<x<1
一元二次方程x2= -2x的根是()
| A.x = 2 |
| B.x = -2 |
| C.x1 = 0,x2 = 2 |
| D.x1 = 0,x2 = -2 |
某商店准备进一批季节性小家电,每个进价为40元,经市场预测,销售定价为50元,可售出400个;定价每增加1元,销售量将减少10个.设每个定价增加x元.
(1)写出售出一个可获得的利润是 元.(用含x的代数式表示)
(2)商店若准备获得利润6000元,并且使进货量较少,则每个定价为多少元?
已知关于x的一元二次方程x2-6x+k=0有两个实数根.
(1)求k的取值范围;
(2)如果k取符合条件的最大整数,且一元二次方程x2-6x+k=0与x2+mx-1=0有一个相同的根,求常数m的值.
如图,公园要在一块长为100米,宽为 80 米的矩形场地上修建三条宽度相等的道路,其中两条 纵向,一条横向,横向道路与纵向道路垂直.剩余部分摆放不同的花卉,要使摆放花卉面积为7488m2,则道路的宽为多少米?设道路的宽为 x 米,则可列方程为()
| A.100×80-100x-80×2x="7488" |
| B.(100-2x)(80-x)="7488" |
| C.(100-2x)(80-x)+2x2="7488" |
| D.100x+80×2x=512 |