对某一个函数给出如下定义:若存在实数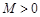 ,对于任意的函数值
,对于任意的函数值 ,都满足
,都满足 ,则称这个函数是有界函数,在所有满足条件的
,则称这个函数是有界函数,在所有满足条件的 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
(1)分别判断函数
 和
和 是不是有界函数?若是有界函数,求其边界值;
是不是有界函数?若是有界函数,求其边界值;
(2)若函数
 的边界值是2,且这个函数的最大值也是2,求
的边界值是2,且这个函数的最大值也是2,求 的取值范围;
的取值范围;
(3)将函数 的图象向下平移
的图象向下平移 个单位,得到的函数的边界值是
个单位,得到的函数的边界值是 ,当
,当 在什么范围时,满足
在什么范围时,满足 ?
?
南菁中学的高中部在敔山湾校区,初中部在老校区,学校学生会在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知敔山湾校区的每位高中学生往返车费是6元,每人每天可栽植5棵树;老校区的每位初中学生往返车费是10元,每人每天可栽植3棵树.要求初高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不得超过210元.要使本次活动植树最多,初高中各有多少学生参加?最多植树多少棵?
(1)阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为|AB|.当A、B两点中有一点在原点时,不妨设点A在原点,如图1-1-1,|AB|="|OB|=|b|=|a-b|" 当A、B两点都不在原点时,
①如图1-1-2,点A、B都在原点的右边|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
②如图1-1-3,点A、B都在原点的左边,|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;
③如图1-1-4,点A、B在原点的两边,|AB|=|OB|-|OA|=|b|-|a|=-b-(-a)=|a-b|;
综上,数轴上A、B两点之间的距离|AB|=|a-b|.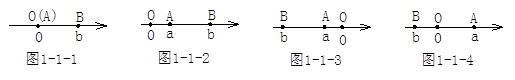
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是 ▲,数轴上表示-2和-5的两点之间的距离是 ▲,
数轴上表示1和-3的两点之间的距离是 ▲;
②数轴上表示x和-1的两点A和B之间的距离是 ▲,如果|AB|=3,那么x ▲;
③当代数式|x+2|十|x-5|取最小值时,相应的x的取值范围是 ▲
④解方程∣x+2∣+∣x-5∣=9
十一届全国人大常委会第二十次会议审议的个人所得税法自2011年9月1日起正式实施,新税法将个人所得税的起征点由原来每月2000元提高到3500元,并将9级超额累进税率修改为7级,新旧两种征税方法的1~5级税率情况见下表:
| 税级 |
原征税方法 |
新征税方法 |
||||
| 月应纳税额x |
税率 |
速算扣除数 |
月应纳税额x |
税率 |
速算扣除数 |
|
| 1 |
x≤500 |
5% |
0 |
x≤1 500 |
3% |
0 |
| 2 |
500<x≤2000 |
10% |
25 |
1500<x≤4500 |
10% |
▲ |
| 3 |
2000<x≤5000 |
15% |
125 |
4500<x≤9000 |
20% |
▲ |
| 4 |
5000<x≤20000 |
20% |
375 |
9000<x≤35000 |
25% |
1005 |
| 5 |
20000<x≤40000 |
25% |
1375 |
35000<x≤55 000 |
30% |
2755 |
注:“月应纳税额”为个人每月收入中超出起征点应该纳税部分的金额.
“速算扣除数”是为快捷简便计算个人所得税而设定的一个数.
例如:按原个人所得税法的规定,某人去年3月的应纳税额为2600元,他应缴税款可以用下面两种方法之一来计算:
方法一:按1~3级超额累进税率计算,即500×5%+1500×10%十600×15%=265(元).
方法二:用“月应纳税额x适用税率一速算扣除数”计算,即2600×15%一l25=265(元)。
(1)请把表中空缺的“速算扣除数”填写完整;
(2)甲去年3月缴了个人所得税1060元,若按“新税法”计算,则他应缴税款多少元?
(3)乙今年3月按“新税法”缴了个人所得税2千多元,比去年3月按“原税法”所缴个人所得税少了155元(今年与去年收入不变),那么乙今年3月所缴税款的具体数额为多少元?