(乐山)“六一”期间,小张购进100只两种型号的文具进行销售,其进价和售价之间的关系如下表:
(1)小张如何进货,使进货款恰好为1300元?
(2)要使销售文具所获利润最大,且所获利润不超过进货价格的40%,请你帮小张设计一个进货方案,并求出其所获利润的最大值.
利用加减消元法解方程组 ,下列做法正确的是( )
,下列做法正确的是( )
| A.要消去y,可以将①×5+②×2 |
| B.要消去x,可以将①×3+②×(﹣5) |
| C.要消去y,可以将①×5+②×3 |
| D.要消去x,可以将①×(﹣5)+②×2 |
为了保护生态平衡,绿化环境,国家大力鼓励“退耕还林、还草”,其补偿政策如表(一);某农户承包了一片山坡地种树种草,所得到国家的补偿如表(二).问:该农户种树、种草各多少亩?
表(一)种树、种草每亩每年补粮补钱情况表
| |
种树 |
种草 |
| 补粮 |
150千克 |
100千克 |
| 补钱 |
200元 |
150元 |
表(二)该农户收到乡政府下发的当种树种草亩数及年补偿通知单
| 种树、种草 |
补粮 |
补钱 |
| 30亩 |
4000千克 |
5500元 |
某超市用3000元购进某种干果销售,由于销售状况良好,超市又调拨9000元资金购进该种干果,但这次的进价比第一次的进价提高了20%,购进干果数量是第一次的2倍还多300千克.
(1)该种干果的第一次进价是每千克多少元?
(2)如果超市按每千克9元的价格出售,当大部分干果售出后,余下的600千克按售价的8折售完,超市销售这种干果共盈利多少元?
某服装店用6000元购进A,B两种新式服装,按标价售出后可获得毛利润3800元(毛利润=售价-进价),这两种服装的进价、标价如下表所示:
| 类型 价格 |
A型 |
B型 |
| 进价(元/件) |
60 |
100 |
| 标价(元/件) |
100 |
160 |
(1)求这两种服装各购进的件数;
(2)如果A中服装按标价的8折出售,B中服装按标价的7折出售,那么这批服装全部售完后,服装店比按标价售出少收入多少元?
阅读下列材料:
解答“已知x﹣y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x﹣y=2,又∵x>1,∴y+2>1,即y>﹣1
又y<0,∴﹣1<y<0.…①
同理得:1<x<2.…②
由①+②得﹣1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组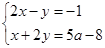 的解都为非负数.
的解都为非负数.
(1)求a的取值范围;
(2)已知2a﹣b=1,且,求a+b的取值范围;
(3)已知a﹣b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示)
已知: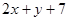 的立方根是3,16的算术平方根是
的立方根是3,16的算术平方根是 ,求:
,求:
(1)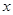 、
、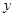 的值;
的值;
(2)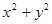 的平方根.
的平方根.
若方程组 的解x,y满足0<x+y<1,则k的取值范围是( )
的解x,y满足0<x+y<1,则k的取值范围是( )
| A.﹣1<k<0 | B.﹣4<k<0 | C.0<k<8 | D.k>﹣4 |