为鼓励居民节约用电,我市自2012年以来对家庭用电收费实行阶梯电价,即每月对每户居民的用电量分为三个档级收费,第一档为用电量在180千瓦时(含180千瓦时)以内的部分,执行基本价格;第二档为用电量在180千瓦时到450千瓦时(含450千瓦时)的部分,实行提高电价;第三档为用电量超出450千瓦时的部分,执行市场调节价格.我市一位同学家今年2月份用电330千瓦时,电费为213元,3月份用电240千瓦时,电费为150元.已知我市的一位居民今年4、5月份的家庭用电量分别为160和 410千瓦时,请你依据该同学家的缴费情况,计算这位居民4、5月份的电费分别为多少元?
利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是 ( ) 
| A.73cm | B.74cm | C.75cm | D.76cm |
去冬今春,某市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(本题10分)我校八年级举行英语风采演讲比赛,派两位老师去超市购买笔记本作为奖品.据了解,该超市的甲、乙两种笔记本的价格分别是10元和6元,他们准备购买这两种笔记本共30本.
(1)若这两位老师计划用220元购买奖品,则能买这两种笔记本各多少本?
(2) 若他们根据演讲比赛的设奖情况,决定所购买的甲种笔记本的数量不多于乙种笔记本数量的 ,但又多于乙种笔记本数量的
,但又多于乙种笔记本数量的 ,若设他们买甲种笔记本x本,买这两种笔记本共花费y元.
,若设他们买甲种笔记本x本,买这两种笔记本共花费y元.
①求出y(元)关于x(本)的函数关系式;
②问购买这两种笔记本各多少时,花费最少,此时的花费是多少元?
兰新铁路的通车,圆了全国人民的一个梦,坐上火车去观赏青海门源百里油菜花海,感受大美青海独特的高原风光,暑假某校准备组织学生、老师到门源进行社会实践,为了便于管理,师生必须乘坐在同一列高铁上,根据报名人数,若都买一等座单程火车票需2340元,若都买二等座单程火车票花钱最少,则需1650元: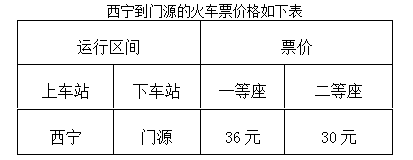

(1)参加社会实践的学生、老师各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(参加社会实践的学生人数<x<参加社会实践的总人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐并且总费用最低的前提下,请你写出购买火车票的总费用(单程)y与x之间的函数关系式.
2015年5月,某县突降暴雨,造成山体滑坡,挢梁垮塌,房屋大面积受损,该省民政厅急需将一批帐篷送往灾区.现有甲、乙两种货车,己知甲种货车比乙种货车每辆车多装20件帐篷,且甲种货车装运1000件帐篷所用车辆与乙种货车装运800件帐蓬所用车辆相等.
(1)求甲、乙两种货车每辆车可装多少件帐蓬?
(2)如果这批帐篷有1490件,用甲、乙两种汽车共16辆来装运,甲种车辆刚好装满,乙种车辆最后一辆只装了50件,其它装满,求甲、乙两种汽车各有多少辆?
梧州市特产批发市场有龟苓膏粉批发,其中A品牌的批发价是每包20元,B品牌的批发价是每包25元,小王需购买A、B两种品牌的龟苓膏共1000包.
(1)若小王按需购买A、B两种品牌龟苓膏粉共用22000元,则各购买多少包?
(2)凭会员卡在此批发市场购买商品可以获得8折优惠,会员卡费用为500元.若小王购买会员卡并用此卡按需购买1000包龟苓膏粉,共用了y元,设A品牌买了x包,请求出y与x之间的函数关系式.
(3)在(2)中,小王共用了20000元,他计划在网店包邮销售这批龟苓膏粉,每包龟苓膏粉小王需支付邮费8元,若每包销售价格A品牌比B品牌少5元,请你帮他计算,A品牌的龟苓膏粉每包定价不低于多少元时才不亏本(运算结果取整数)?
理数学兴趣小组在探究如何求tan15°的值,经过思考、讨论、交流,得到以下思路:
思路一 如图1,在Rt△ABC中,∠C=90°,∠ABC=30°,延长CB至点D,使BD=BA,连接AD.设AC=1,则BD=BA=2,BC=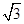 .tanD=tan15°=
.tanD=tan15°= =
=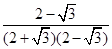 =
= .
.
思路二 利用科普书上的和(差)角正切公式:tan(α±β)=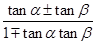 .假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=
.假设α=60°,β=45°代入差角正切公式:tan15°=tan(60°﹣45°)=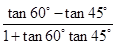 =
= =
= .
.
思路三 在顶角为30°的等腰三角形中,作腰上的高也可以…
思路四 …
请解决下列问题(上述思路仅供参考).
(1)类比:求出tan75°的值;
(2)应用:如图2,某电视塔建在一座小山上,山高BC为30米,在地平面上有一点A,测得A,C两点间距离为60米,从A测得电视塔的视角(∠CAD)为45°,求这座电视塔CD的高度;
(3)拓展:如图3,直线 与双曲线
与双曲线 交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
交于A,B两点,与y轴交于点C,将直线AB绕点C旋转45°后,是否仍与双曲线相交?若能,求出交点P的坐标;若不能,请说明理由.
目前节能灯在城市已基本普及,今年全省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
| |
进价(元/只) |
售价(元/只) |
| 甲型 |
25 |
30 |
| 乙型 |
45 |
60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时最大利润为多少元?
(本小题满分10分)
已知甲、乙两种矿石中均含有金属A,其含量及每吨原料的购买单价如下表所示:
| |
金属A含量 |
单价(万元/吨) |
| 甲矿石 |
5% |
2 5 |
| 乙矿石 |
8% |
6 |
已知用甲矿石提取每千克金属A要排放废气1吨,用乙矿石提取每千克金属A要排放废气0 5吨,若某厂要提取金属A20千克,并要求废气排放不超过16吨,问:该厂购买这两种原料的费用最少是多少万元?
目前节能灯在城市已基本普及,今年湖南省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共1200只,这两种节能灯的进价、售价如下表:
| |
进价(元/只) |
售价(元/只) |
| 甲型 |
25 |
30 |
| 乙型 |
45 |
60 |
(1)如何进货,进货款恰好为46000元?
(2)如何进货,商场销售完节能灯时获利最多且不超过进货价的30%,此时利润为多少元
某工厂计划生产A、B两种产品共60件,需购买甲、乙两种材料.生产一件A产品需甲种材料4千克,乙种材料1千克;生产一件B产品需甲、乙两种材料各3千克.经测算,购买甲、乙两种材料各1千克共需资金60元;购买甲种材料2千克和乙种材料3千克共需资金155元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不能超过10000元,且生产B产品要超过38件,问有哪几种符合条件的生产方案?
(3)在(2)的条件下,若生产一件A产品需加工费40元,若生产一件B产品需加工费50元,应选择哪种生产方案,才能使生产这批产品的成本最低?请直接写出方案。
(8分)我们用 表示不大于
表示不大于 的最大整数,例如:
的最大整数,例如: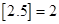 ,
, ,
, ;用
;用 表示大于
表示大于 的最小整数,例如:
的最小整数,例如: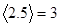 ,
,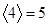 ,
, 。解决下列问题:
。解决下列问题:
(1) = ,
= , = .
= .
(2)若 =3则
=3则 的取值范围是 ;若
的取值范围是 ;若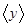 =-2,则
=-2,则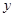 的取值范围是 .
的取值范围是 .
(3)已知 ,
,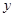 满足方程组
满足方程组 ,求
,求 ,
,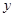 的取值范围.
的取值范围.