某服装商预测一种应季衬衫能畅销市场,就用8000元购进一批衬衫,面市后果然供不应求,服装商又用17600元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了8元.商家销售这种衬衫时每件定价都是100元,最后剩下10件按8折销售,很快售完.在这两笔生意中,商家共盈利多少元?
某中学新建了一栋四层的教学楼,每层楼有10间教室,进出这栋教学楼共有4个门,其中两个正门大小相同,两个侧门大小也相同.安全检查中,对4个门进行了测试,当同时开启一个正门和两个侧门时,2分钟内可以通过560名学生;当同时开启一个正门和一个侧门时,4分钟内可以通过800名学生.
(1)求平均每分钟一个正门和一个侧门各可以通过多少名学生?
(2)检查中发现,出现紧急情况时,因学生拥挤,出门的效率将降低20%,安全检查规定:在紧急情况下全楼的学生应在5分钟内通过这4个门安全撤离,假设这栋教学大楼每间教室最多有45名学生,问:该教学楼建造的这4个门是否符合安全规定?请说明理由.
如图,在平面直角坐标系xOy中,四边形ABCD是菱形,顶点A.C.D均在坐标轴上,且AB=5,sinB= .
.
(1)求过A.C. D三点的抛物线的解析式;
(2)记直线AB的解析式为y1=mx+n,(1)中抛物线的解析式为y2=ax2+bx+c,求当y1<y2时,自变量x的取值范围;
(3)设直线AB与(1)中抛物线的另一个交点为E,P点为抛物线上A.E两点之间的一个动点,当P点在何处时,△PAE的面积最大?并求出面积的最大值.
2012年6月5日是第40个世界环境日,世界环境日的主题为“多个物种、一颗星球、一个未来”。为了响应节能减排的号召,某品牌汽车店准备购进A型(电动汽车)和B型(太阳能汽车)两种不同型号的汽车共16辆,以满足广大支持环保的购车者的需求。市场营销人员经过市场调查得到如下信息:
| |
成本价(万元/辆) |
售价(万元/辆) |
| A型 |
30 |
32 |
| B型 |
42 |
45 |
(1)若经营者的购买资金不少于576万元且不多于600万元,有哪几种进车方案?
(2)在(1)的前提下,如果你是经营者,并且所进的汽车能全部售出,你会选择哪种进车方案才能使获得的利润最大?最大利润是多少?
(3)假设每台电动汽车每公里的用电费用为0.65元,且两种汽车最大行驶里程均为30万公里,那么从节约资金的角度,你作为一名购车者,将会选购哪一种型号的汽车?并说明理由。
青青商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.若该商场同时购进甲、乙两种商品共100件,恰好用去2700元,求购进的甲、乙两种商品各多少件?
该商场为使甲、乙两种商品共100件的总利润(利润=售价
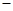 进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;
进价)不少于750元,且不超过760元,请你帮助该商场设计相应的进货方案;在“五·一”黄金周期间,该商场对甲、乙两种商品进行如下优惠促销活动:
| 打折前一次性购物总金额 |
优惠措施 |
| 不超过300元 |
不优惠 |
| 超过300元且不超过400元 |
售价打九折 |
| 超过400元 |
售价打八折 |
按上述优惠条件,若小王第一天只购买甲种商品一次性付款200元,第二天只购买乙种商品打折后一次性付款324元,那么这两天他在该商场购买甲、乙两种商品一共多少件?(通过计算求出所有符合要求的结果)