初中数学有理数无理数的概念与运算解答题

将1，2，3……100，这100个自然数任意分成50组，每组两个数，将其中一个数记为a，另一个数记为b，代入代数式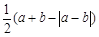中计算，求出其结果，50组都代入后可得50个值，求这50个值的和的最小值（请简要说明理由）．

把表示下列各数的点画在数轴上，再按从小到大的顺序，用＂＜＂号把这些数连接起来：.

某公司今年第一季度收入与支出情况如表所示（单位：万元）
请问： (1)该公司今年第一季度总收入与总支出各多少万元？
(2)如果收入用正数表示，则总收入与总支出应如何表示？
(3)该公司第一季度利润为多少万元？

月份	一月	二月	三月
收入	32	48	50
支出	12	13	10

 

（本题 8 分）若a、b互为相反数, c是最小的非负数, d是最大的负整数,
求(a+b)d+d－c的值.

（本题8分）湖州市出租车收费标准如下：3公里以内（含3公里）为起步价收费10元，超过3公里的部分每公里收费2元。超过起步里程10公里以上的部分加收50%，即每公里3元。（不足1公里以1公里计算）
（1）小明一次乘坐出租车行驶4.3公里应付车费多少元？
（2）若小明乘坐出租车行驶15.2公里，问应付车费多少元？
（3）小明家距离学校13.3千米，周末小明身边带了32元钱，则小明从学校坐出租车到家的钱够吗？如果够，还剩多少钱？如果不够他至少要先走多少公里路？

（本小题6分）画一条数轴，把 -1，，2各数和它们的相反数在数轴上表示出来，并比较它们的大小，用“<”号连接。

（本小题6分）把下列各数填在相应的表示集合的大括号内：
－2 ，π，，，，－0.3，1.7，，0 ， 1.1010010001……（每两个1之间依次多一个0）
整 数{                                            ……}
负分数{                                             ……}
无理数{                                             ……}

（本小题8分）出租车司机小傅某天下午营运全是在东西走向的大道上行驶的，如果规定向东为正，行车里程（单位：km）如下：
+11，-2，+3，+10，-11，+5，-15，-8
（1）当把最后一名乘客送到目的地时，小傅距离出车地点的距离为多少？
（2）若每千米的营运额为7元，成本为1.5元/km，则这天下午他盈利多少元？

（本小题满分12分）某地区的海产品由A地运往B地，汽车货运公司和铁路货运公司均开办海产品运输业务。已知运输路程为120km，汽车和火车的速度分别为60km/h和100km/h，两货运公司的收费项目及收费标准如下表所示：

运输工具	运输费 （元/吨·千米）	冷藏费 （元/吨·小时）	过路费 （元）	装卸及 管理费（元）
汽车	2	5	200	0
火车	1.8	5	0	1600

注：“元/吨·千米”表示每吨货物每千米的运费；
“元/吨·小时”表示每吨货物每小时冷藏费。
若该批发商待运的海产品有30吨，为节省运费，应选哪个货运公司？
若该批发商待运的海产品有60吨，他又该选哪个货运公司较为合算？
当该批发商有多少海产品时，无论选哪家都一样？

结合数轴与绝对值的知识回答下列问题：

数轴上表示1和4的两点之间的距离是_________；表示－3和2的两点之间的距离是_________；表示－5和－4的两点之间的距离是_________；一般地，数轴上表示数和数的两点之间的距离等于_____________．
如果表示数和－2的两点之间的距离是3，那么=__________．
若数轴上表示数的点位于－4与2之间，求的值；
当______时，的值最小，最小值是____________

同学们，我们曾经研究过n×n的正方形网格，得到了网格中正方形的总数的表达式为1²+2²+3²+…+n²．但n为100时，应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题．首先，通过探究我们已经知道0×1+1×2+2×3+…+(n—1)×n=n(n+1)(n—1)时，我们可以这样做：
(1)观察并猜想：
1²+2²=(1+0)×1+(1+1)×2=1+0×1+2+1×2=(1+2)+(0×1+1×2)
1²+2²+3²=(1+0)×1+(1+1)×2+(1+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
1²+2²+3²+4²=(1+0)×1+(1+1)×2+(1+2)×3+               
=1+0×1+2+1×2+3+2×3+                        
=(1+2+3+4)+(                                  )
……
(2)归纳结论：
1²+2²+3²+…+n²=(1+0)×1+(1+1)×2+(1+2)×3+…+n
=1+0×1+2+1×2+3+2×3+…+n+(n一1)×n
=(                      ) +
=                      +                                 
=×                     
(3)实践应用：
通过以上探究过程，我们就可以算出当n为100时，正方形网格中正方形的总个数是              ．

如图，一只蚂蚁从点沿数轴向右直爬2个单位到达点，点表示，设点所表示的数为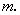

求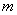的值
求的值．

观察下面的变形规律：
 ＝1－； ＝－；＝－；……
解答下面的问题：
（1）若n为正整数，请你猜想＝                  ；
（2）证明你猜想的结论；
（3）求和：＋＋＋…＋ .

阅读探究有关个位数是5的整数的平方简便计算问题.
观察下列算式：
15²=1×2×100＋25=225；25²=2×3×100＋25=625；35²=3×4×100＋25=1225……
请你写出95²的简便计算过程及结果；
其实这种方法也可以推广到个位数是5的三位数的平方，证明略.
① 请你写出115²的简便计算过程及结果.
② 用计算或说理的方式确定985²－895²的结果末两位数字是多少？
已知一个个位数是5的整数的平方是354025，请用方程的相关知识求这个数.

在数轴上表示a，0，1，b四个数的点如图所示，已知O为AB的中点.
求＋＋的值.