初中数学列表法与树状图法试题

我省某地区为了了解2016年初中毕业生毕业去向，对部分九年级学生进行了抽样调查，就九年级学生毕业后的四种去向： $A$．读普通高中； $B$．读职业高中； $C$．直接进入社会就业； $D$．其他（如出国等）进行数据统计，并绘制了两幅不完整的统计图（如图1，如图2）

（1）填空：该地区共调查了　   　名九年级学生；

（2）将两幅统计图中不完整的部分补充完整；

（3）若该地区2016年初中毕业生共有3500人，请估计该地区今年初中毕业生中读普通高中的学生人数；

（4）老师想从甲，乙，丙，丁4位同学中随机选择两位同学了解他们毕业后的去向情况，请用画树状图或列表的方法求选中甲同学的概率．

在学校组织的义务植树活动中，甲、乙两组各四名同学的植树棵数如下，甲组：9，9，11，10；乙组：9，8，9，10；分别从甲、乙两组中随机选取一名同学，则这两名同学的植树总棵数为19的概率 　　．

某校在践行“社会主义核心价值观”演讲比赛中，对名列前20名的选手的综合分数m进行分组统计，结果如表所示：

组号	分组	频数
一	6≤m＜7	2
二	7≤m＜8	7
三	8≤m＜9	a
四	9≤m≤10	2

（1）求a的值；

（2）若用扇形图来描述，求分数在8≤m＜9内所对应的扇形图的圆心角大小；

（3）将在第一组内的两名选手记为：A₁、A₂，在第四组内的两名选手记为：B₁、B₂，从第一组和第四组中随机选取2名选手进行调研座谈，求第一组至少有1名选手被选中的概率（用树状图或列表法列出所有可能结果）．

为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩用如图的折线统计图表示：（甲为实线，乙为虚线）

（1）依据折线统计图，得到下面的表格：

射击次序（次 $)$	1	2	3	4	5	6	7	8	9	10
甲的成绩（环 $)$	8	9	7	9	8	6	7	$a$	10	8
乙的成绩（环 $)$	6	7	9	7	9	10	8	7	$b$	10

其中 $a=$　， $b=$　　；

（2）甲成绩的众数是　　环，乙成绩的中位数是　　环；

（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？

（4）该校射击队要参加市组织的射击比赛，已预选出2名男同学和2名女同学，现要从这4名同学中任意选取2名同学参加比赛，请用列表或画树状图法，求出恰好选到1男1女的概率．

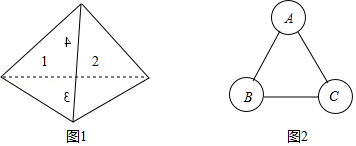
如图1，一枚质地均匀的正四面体骰子，它有四个面，并分别标有1，2，3，4四个数字；如图2，等边三角形 $\mathit{ABC}$ 的三个顶点处各有一个圆圈．丫丫和甲甲想玩跳圈游戏，游戏的规则为：游戏者从圈 $A$ 起跳，每投掷一次骰子，骰子着地的一面点数是几，就沿着三角形的边逆时针方向连续跳跃几个边长．如：若第一次掷得点数为2，就逆时针连续跳2个边长，落到圈 $C$ ；若第二次掷得点数为4，就从圈 $C$ 继续逆时针连续跳4个边长，落到圈 $A$ ．

（1）丫丫随机掷一次骰子，她跳跃后落回到圈 $A$ 的概率为 　　；

（2）丫丫和甲甲一起玩跳圈游戏：丫丫随机投掷一次骰子，甲甲随机投掷两次骰子，都以最终落回到圈 $A$ 为胜者．这个游戏规则公平吗？请说明理由．

一个布袋里装有4个只有颜色不同的球，其中3个红球，1个白球．从布袋里摸出1个球，记下颜色后放回，搅匀，再摸出1个球，则两次摸到的球都是红球的概率是 $($　　 $)$

A． $\frac{1}{16}$B． $\frac{1}{2}$C． $\frac{3}{8}$D． $\frac{9}{16}$

已知电流在一定时间段内正常通过电子元件" "的概率是0.5；则在一定时间段内，由该元件组成的图示电路 $A$ 、 $B$ 之间，电流能够正常通过的概率是 $($ 　　 $)$

A．

0.75

B．

0.525

C．

0.5

D．

0.25

在中国共产党成立100周年之际，我市某中学开展党史学习教育活动．为了了解学生学习情况，在七年级随机抽取部分学生进行测试，并依据成绩（百分制）绘制出以下两幅不完整的统计图．请根据图中信息回答下列问题：

（1）本次抽取调查的学生共有 　　人，扇形统计图中表示 C等级的扇形圆心角度数为 　　．

（2） A等级中有2名男生，2名女生，从中随机抽取2人参加学校组织的知识问答竞赛，请用画树状图或列表的方法，求恰好抽到一男一女的概率．

看了《田忌赛马》故事后，小杨用数学模型来分析：齐王与田忌的上中下三个等级的三匹马记分如表，每匹马只赛一场，两数相比，大数为胜，三场两胜则赢．已知齐王的三匹马出场顺序为10，8，6．若田忌的三匹马随机出场，则田忌能赢得比赛的概率为 　　．

马匹 姓名	下等马	中等马	上等马
齐王	6	8	10
田忌	5	7	9

如图在三条横线和三条竖线组成的图形中，任选两条横线和两条竖线都可以围成一个矩形，从这些矩形中任选一个，则所选矩形含点 $A$ 的概率是 $($ 　　 $)$

A．

$\frac{1}{4}$

B．

$\frac{1}{3}$

C．

$\frac{3}{8}$

D．

$\frac{4}{9}$

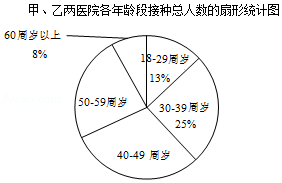
“此生无悔入华夏，来世再做中国人！”自疫情暴发以来，我国科研团队经过不懈努力，成功地研发出了多种“新冠”疫苗，并在全国范围内免费接种．截止2021年5月18日 $16:20$，全球接种“新冠”疫苗的比例为 $18.29\%$；中国累计接种4.2亿剂，占全国人口的 $29.32\%$．以下是某地甲、乙两家医院5月份某天各年龄段接种疫苗人数的频数分布表和接种总人数的扇形统计图：

	甲医院			乙医院
年龄段	频数	频率	频数		频率
$18-29$周岁	900	0.15	400		0.1
$30-39$周岁	$a$	0.25	1000		0.25
$40-49$周岁	2100	$b$	$c$		0.225
$50-59$周岁	1200	0.2	1200		0.3
60周岁以上	300	0.05	500		0.125

（1）根据上面图表信息，回答下列问题：

①填空： $a=$　　， $b=$　　， $c=$　　；

②在甲、乙两医院当天接种疫苗的所有人员中， $40-49$周岁年龄段人数在扇形统计图中所占圆心角为 　　；

（2）若 $A$、 $B$、 $C$三人都于当天随机到这两家医院接种疫苗，求这三人在同一家医院接种的概率．

为了倡导“节约用水，从我做起”，某市政府决定对该市直属机关200户家庭用水情况进行调查．市政府调查小组随机抽查了其中部分家庭一年的月平均用水量（单位：吨），调查中发现，每户家庭月平均用水量在 $3~7$吨范围内，并将调查结果制成了如下尚不完整的统计表：

月平均用水量（吨 $)$	3	4	5	6	7
频数（户数）	4	$a$	9	10	7
频率	0.08	0.40	$b$	$c$	0.14

请根据统计表中提供的信息解答下列问题：

（1）填空： $a=$　　， $b=$　　， $c=$　　．

（2）这些家庭中月平均用水量数据的平均数是 　　，众数是 　　，中位数是 　　．

（3）根据样本数据，估计该市直属机关200户家庭中月平均用水量不超过5吨的约有多少户？

（4）市政府决定从月平均用水量最省的甲、乙、丙、丁四户家庭中，选取两户进行“节水”经验分享．请用列表或画树状图的方法，求出恰好选到甲、丙两户的概率，并列出所有等可能的结果．

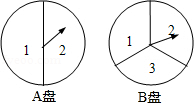
小兰和小颖用下面两个可以自由转动的转盘做游戏，每个转盘被分成面积相等的几个扇形，转动两个转盘各一次，若两次指针所指数字之和小于4，则小兰胜，否则小颖胜（指针指在分界线时重转），这个游戏对双方公平吗？请用树状图或列表法说明理由．

小明和小红玩抛硬币游戏，连续抛两次，小明说：“如果两次都是正面，那么你赢；如果两次是一正一反，则我赢．”小红赢的概率是　　，据此判断该游戏　　（填“公平”或“不公平” $)$．

随着我省“大美青海，美丽夏都”影响力的扩大，越来越多的游客慕名而来．根据青海省旅游局《2015年国庆长假出游趋势报告》绘制了如下尚不完整的统计图．

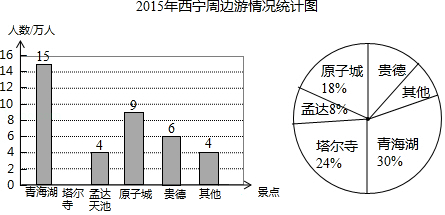
根据以上信息解答下列问题：

（1）2015年国庆期间，西宁周边景区共接待游客　     　万人，扇形统计图中“青海湖”所对应的圆心角的度数是　     　，并补全条形统计图；

（2）预计2016年国庆节将有80万游客选择西宁周边游，请估计有多少万人会选择去贵德旅游？

（3）甲乙两个旅行团在青海湖、塔尔寺、原子城三个景点中，同时选择去同一个景点的概率是多少？请用画树状图或列表法加以说明，并列举所有等可能的结果．