初中数学频数（率）分布直方图试题

如图是九（1）班45名同学每周课外阅读时间的频数直方图（每组含前一个边界值，不含后一个边界值）．由图可知，人数最多的一组是 $($　　 $)$

A． $2~4$小时B． $4~6$小时C． $6~8$小时D． $8~10$小时

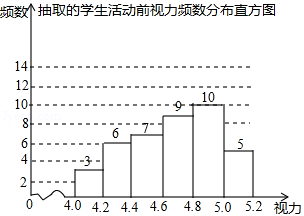
为了保护视力，学校开展了全校性的视力保健活动，活动前，随机抽取部分学生，检查他们的视力，结果如图所示（数据包括左端点不包括右端点，精确到 $0.1)$；活动后，再次检查这部分学生的视力，结果如表所示．

分组	频数
$4.0⩽x<4.2$	2
$4.2⩽x<4.4$	3
$4.4⩽x<4.6$	5
$4.6⩽x<4.8$	8
$4.8⩽x<5.0$	17
$5.0⩽x<5.2$	5

（1）求所抽取的学生人数；

（2）若视力达到4.8及以上为达标，估计活动前该校学生的视力达标率；

（3）请选择适当的统计量，从两个不同的角度分析活动前后相关数据，并评价视力保健活动的效果．

为了掌握八年级数学考试卷的命题质量与难度系数，命题组教师赴外地选取一个水平相当的八年级班级进行预测，将考试成绩分布情况进行处理分析，制成频数分布表如下（成绩得分均为整数） $:$

组别	成绩分组	频数	频率
1	$47.5~59.5$	2	0.05
2	$59.5~71.5$	4	0.10
3	$71.5~83.5$	$a$	0.2
4	$83.5~95.5$	10	0.25
5	$95.5~107.5$	$b$	$c$
6	$107.5~120$	6	0.15
合计		40	1.00

根据表中提供的信息解答下列问题：

（1）频数分布表中的 $a=$　　， $b=$　　， $c=$　　；

（2）已知全区八年级共有200个班（平均每班40人），用这份试卷检测，108分及以上为优秀，预计优秀的人数约为　　，72分及以上为及格，预计及格的人数约为　　，及格的百分比约为　　；

（3）补充完整频数分布直方图．

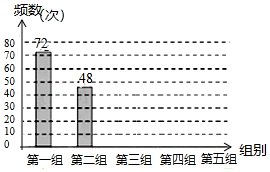
某网络约车公司近期推出了”520专享”服务计划，即要求公司员工做到“5星级服务、2分钟响应、0客户投诉”，为进一步提升服务品质，公司监管部门决定了解“单次营运里程”的分布情况．老王收集了本公司的5000个“单次营运里程”数据，这些里程数据均不超过25（公里），他从中随机抽取了200个数据作为一个样本，整理、统计结果如下表，并绘制了不完整的频数分布直方图（如图）．

组别	单次营运里程“ $x$”（公里）	频数
第一组	$0<x⩽5$	72
第二组	$5<x⩽10$	$a$
第三组	$10<x⩽15$	26
第四组	$15<x⩽20$	24
第五组	$20<x⩽25$	30

根据统计表、图提供的信息，解答下面的问题：

（1）①表中 $a=$　　；②样本中“单次营运里程”不超过15公里的频率为　　；③请把频数分布直方图补充完整；

（2）请估计该公司这5000个“单次营运里程”超过20公里的次数；

（3）为缓解城市交通压力，维护交通秩序，来自某市区的4名网约车司机 $(3$男1女）成立了“交通秩序维护”志愿小分队，若从该小分队中任意抽取两名司机在某一路口维护交通秩序，请用列举法（画树状图或列表）求出恰好抽到“一男一女”的概率．

在一次社会调查活动中，小李收集到某“健步走运动”团队20名成员一天行走的步数，记录如下：

5640	6430	6520	6798	7325
8430	8215	7453	7446	6754
7638	6834	7326	6830	8648
8753	9450	9865	7290	7850

对这20个数据按组距1000进行分组，并统计整理，绘制了如下不完整的统计图表，步数分布统计图．

组别	步数分组	频数
$A$	$5500⩽x<6500$	$m$
$B$	$6500⩽x<7500$	10
$C$	$7500⩽x<8500$	4
$D$	$8500⩽x<9500$	$n$
$E$	$9500⩽x<10500$	1

根据以上信息解答下列问题：

（1）填空： $m=$　　， $n=$　　；

（2）请补全条形统计图；

（3）这20名“健步走运动”团队成员一天行走的步数的中位数落在　　组；

（4）若该团队共有200人，请估计其中一天行走步数少于8500步的人数．

红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查，从试验田中随机抽取了30株，得到的数据如下（单位：颗） $:$

182	195	201	179	208	204	186	192	210	204
175	193	200	203	188	197	212	207	185	206
188	186	198	202	221	199	219	208	187	224

（1）对抽取的30株水稻稻穗谷粒数进行统计分析，请补全下表中空格，并完善直方图：

谷粒颗数	$175⩽x<185$	$185⩽x<195$	$195⩽x<205$	$205⩽x<215$	$215⩽x<225$
频数		8	10		3
对应扇形 图中区域		$D$	$E$		$C$

如图所示的扇形统计图中，扇形 $A$对应的圆心角为　　度，扇形 $B$对应的圆心角为　　度；

（2）该试验田中大约有3000株水稻，据此估计，其中稻穗谷粒数大于或等于205颗的水稻有多少株？

现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整） $:$

步数	频数	频率
$0⩽x<4000$	8	$a$
$4000⩽x<8000$	15	0.3
$8000⩽x<12000$	12	$b$
$12000⩽x<16000$	$c$	0.2
$16000⩽x<20000$	3	0.06
$20000⩽x<24000$	$d$	0.04

请根据以上信息，解答下列问题：

（1）写出 $a$， $b$， $c$， $d$的值并补全频数分布直方图；

（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？

（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步）的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．

“品中华诗词，寻文化基因”．某校举办了第二届“中华诗词大赛”，将该校八年级参加竞赛的学生成绩统计后，绘制了如下不完整的频数分布统计表与频数分布直方图．

频数分布统计表

组别	成绩 $x$（分）	人数	百分比
$A$	$60⩽x<70$	8	$20\%$
$B$	$70⩽x<80$	16	$m\%$
$C$	$80⩽x<90$	$a$	$30\%$
$D$	$90⩽x⩽100$	4	$10\%$

请观察图表，解答下列问题：

（1）表中 $a=$　     　， $m=$　      　；

（2）补全频数分布直方图；

（3） $D$组的4名学生中，有1名男生和3名女生．现从中随机抽取2名学生参加市级竞赛，则抽取的2名学生恰好是一名男生和一名女生的概率为　    　．

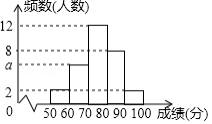
为了解某次“小学生书法比赛”的成绩情况，随机抽取了30名学生的成绩进行统计，并将统计情况绘成如图所示的频数分布直方图，已知成绩 $x$（单位：分）均满足“ $50⩽x<100$”．根据图中信息回答下列问题：

（1）图中 $a$的值为　      　；

（2）若要绘制该样本的扇形统计图，则成绩 $x$在“ $70⩽x<80$”所对应扇形的圆心角度数为　     　度；

（3）此次比赛共有300名学生参加，若将“ $x⩾80$”的成绩记为“优秀”，则获得“优秀“的学生大约有　      　人：

（4）在这些抽查的样本中，小明的成绩为92分，若从成绩在“ $50⩽x<60$”和“ $90⩽x<100$”的学生中任选2人，请用列表或画树状图的方法，求小明被选中的概率．

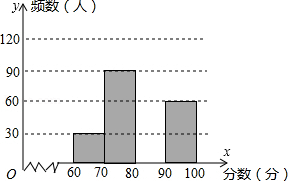
为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示．请根据图表信息解答下列问题：

组别	分数段（分 $)$	频数	频率
$A$组	$60⩽x<70$	30	0.1
$B$组	$70⩽x<80$	90	$n$
$C$组	$80⩽x<90$	$m$	0.4
$D$组	$90⩽x<100$	60	0.2

（1）在表中： $m=$　　， $n=$　　；

（2）补全频数分布直方图；

（3）小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在　　组；

（4）4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中 $A$、 $C$两组学生的概率是多少？并列表或画树状图说明．

在大课间活动中，体育老师随机抽取了八年级甲、乙两个班部分女同学进行仰卧起坐的测试，并对成绩进行统计分析，绘制了频数分布表和统计图，请你根据图表中的信息完成下列问题：

分　　组	频数	频率
第一组 $(0⩽x<15)$	3	0.15
第二组 $(15⩽x<30)$	$a$	0.3
第三组 $(30⩽x<45)$	7	0.35
第四组 $(45⩽x<60)$	4	$b$

（1）频数分布表中 $a=$　      　， $b=$　      　，并将统计图补充完整；

（2）如果该校八年级共有女生180人，估计仰卧起坐一分钟完成30或30次以上的女学生有多少人；

（3）已知第一组中只有一个甲班同学，第四组中只有一个乙班同学，老师随机从这两个组中各选一名学生谈心得体会，用树状图或列表求所选两人正好都是甲班学生的概率．

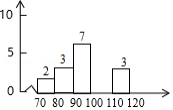
从某校初三年级中随机抽查若干名学生摸底检测的数学成绩（满分为120分），制成如图的统计直方图，已知成绩在 $80~90$分（含80分，不含90分）的学生为抽查人数的 $15\%$，且规定成绩大于或等于100分为优秀．

（1）求被抽查学生人数及成绩在 $100~110$分的学生人数 $m$；

（2）在被抽查的学生中任意抽取1名学生，则这名学生成绩为优秀的概率；

（3）若该校初三年级共有300名学生，请你估计本次检测中该校初三年级数学成绩为优秀的人数．

某校为组织代表队参加市“拜炎帝、诵经典”吟诵大赛，初赛后对选手成绩进行了整理，分成5个小组 $(x$表示成绩，单位：分）， $A$组： $75⩽x<80$； $B$组： $80⩽x<85$； $C$组： $85⩽x<90$； $D$组： $90⩽x<95$； $E$组： $95⩽x<100$．并绘制出如图两幅不完整的统计图．

请根据图中信息，解答下列问题：

（1）参加初赛的选手共有　    　名，请补全频数分布直方图；

（2）扇形统计图中， $C$组对应的圆心角是多少度？ $E$组人数占参赛选手的百分比是多少？

（3）学校准备组成8人的代表队参加市级决赛， $E$组6名选手直接进入代表队，现要从 $D$组中的两名男生和两名女生中，随机选取两名选手进入代表队，请用列表或画树状图的方法，求恰好选中一名男生和一名女生的概率．

随着社会的发展，私家车变得越来越普及，使用节能低油耗汽车，对环保有着非常积极的意义，某市有关部门对本市的某一型号的若干辆汽车，进行了一项油耗抽样实验：即在同一条件下，被抽样的该型号汽车，在油耗 $1L$的情况下，所行驶的路程（单位： $\mathit{km})$进行统计分析，结果如图所示：

（注：记 $A$为 $12~12.5$， $B$为 $12.5~13$， $C$为 $13~13.5$， $D$为 $13.5~14$， $E$为 $14~14.5)$

请依据统计结果回答以下问题：

（1）试求进行该试验的车辆数；

（2）请补全频数分布直方图；

（3）若该市有这种型号的汽车约900辆（不考虑其他因素），请利用上述统计数据初步预测，该市约有多少辆该型号的汽车，在耗油 $1L$的情况下可以行驶 $13\mathit{km}$以上？

某汽车公司为了解某型号汽车在同一条件下的耗油情况，随机抽取了 $n$辆该型号汽车耗油 $1L$所行使的路程作为样本，并绘制了如图不完整的频数分布直方图和扇形统计图．根据题中已有信息，解答下列问题：

（1）求 $n$的值，并补全频数分布直方图；

（2）若该汽车公司有600辆该型号汽车．试估计耗油 $1L$所行使的路程低于 $13\mathit{km}$的该型号汽车的辆数；

（3）从被抽取的耗油 $1L$所行使路程在 $12⩽x<12.5$， $14⩽x<14.5$这两个范围内的4辆汽车中，任意抽取2辆，求抽取的2辆汽车来自同一范围的概率．