如图, 经过平面直角坐标系的原点 ,交 轴于点 ,交 轴于点 ,点 为第二象限内圆上一点.则 的正弦值是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,已知点 是矩形 的对角线 上的一动点,正方形 的顶点 、 都在边 上,若 , ,则 的值

A.等于 B.等于
C.等于 D.随点 位置的变化而变化
比萨斜塔是意大利的著名建筑,其示意图如图所示,设塔顶中心点为点 ,塔身中心线 与垂直中心线 的夹角为 ,过点 向垂直中心线 引垂线,垂足为点 .通过测量可得 、 、 的长度,利用测量所得的数据计算 的三角函数值,进而可求 的大小.下列关系式正确的是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,半径为3的 经过原点 和点 , 是 轴左侧 优弧上一点,则 为
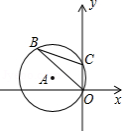
A. B. C. D.
如图,在矩形 中, , , 是 的中点,将 沿直线 翻折,点 落在点 处,连结 ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,边长为1的小正方形构成的网格中,半径为1的 的圆心 在格点上,则 的正切值等于
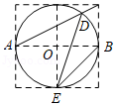
A. B. C.2D.
如图,在 的正方形网格中,每个小正方形的边长都是1, 的顶点都在这些小正方形的顶点上,则 的值为
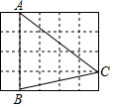
| A. |
|
B. |
|
C. |
|
D. |
|
如图, 是圆锥的母线, 为底面直径,已知 ,圆锥的侧面积为 ,则 的值为
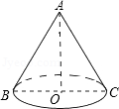
A. B. C. D.
矩形 在平面直角坐标系中的位置如图所示,已知 , ,点 在 轴上,点 在 轴上, 是对角线 上一动点(不与原点重合),连接 ,过点 作 ,交 轴于点 .下列结论:
① ;
②当点 运动到 的中点处时, ;
③在运动过程中, 是一个定值;
④当 为等腰三角形时,点 的坐标为 , .
其中正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
如图,在 中, , 和 关于直线 对称,连接 ,与 相交于点 ,过点 作 ,垂足为 , 相交于点 ,若 , ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图是由边长相同的小正方形组成的网格, , , , 四点均在正方形网格的格点上,线段 , 相交于点 ,则图中 的正切值是

A. B.1C. D.2
如图,面积为24的 中,对角线 平分 ,过点 作 交 的延长线于点 , ,则 的值为

| A. |
|
B. |
|
C. |
|
D. |
|