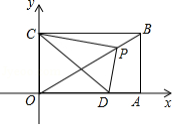
矩形 在平面直角坐标系中的位置如图所示,已知 , ,点 在 轴上,点 在 轴上, 是对角线 上一动点(不与原点重合),连接 ,过点 作 ,交 轴于点 .下列结论:
① ;
②当点 运动到 的中点处时, ;
③在运动过程中, 是一个定值;
④当 为等腰三角形时,点 的坐标为 , .
其中正确结论的个数是
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
相关知识点
推荐套卷
矩形 在平面直角坐标系中的位置如图所示,已知 , ,点 在 轴上,点 在 轴上, 是对角线 上一动点(不与原点重合),连接 ,过点 作 ,交 轴于点 .下列结论:
① ;
②当点 运动到 的中点处时, ;
③在运动过程中, 是一个定值;
④当 为等腰三角形时,点 的坐标为 , .
其中正确结论的个数是

| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |