(本题共8分)阅读下列材料:小昊遇到这样一个问题:如图1,在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,求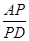 的值.
的值.
小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).请回答: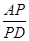 的值为__________.
的值为__________.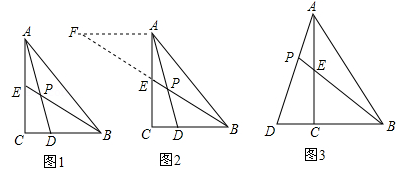
参考小昊思考问题的方法,解决问题:
如图 3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
(1)求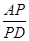 的值;
的值;
(2)若CD=2,则BP=_________________.
(本题共6分)如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
(本题共6分)如图,每个小方格都是边长为1个单位的小正方形,A.B.C三点都是格点(每个小方格的顶点叫格点),其中A(1,8),B(3,8),C(4,7).
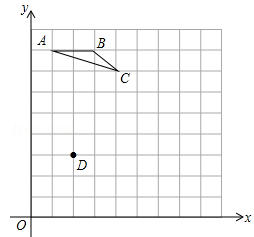
(1)若D(2,3),请在网格图中画一个格点△DEF,使△DEF ∽△ABC,且相似比为2∶1;
(2)求△ABC中AC边上的高;
(3)若△ABC外接圆的圆心为P,则点P的坐标为 .
如图,在Rt△ABC中∠ACB=90°,CD⊥AB于D .已知AC=6,AD=2求AB?
(本小题满分8分)如图,平面直角坐标系中,将含30°的三角尺的直角顶点C落在第二象限.其斜边两端点A、B分别落在x轴、y轴上,且AB=12cm
(1)若OB=6cm.
①求点C的坐标;
②若点A向右滑动的距离与点B向上滑动的距离相等,求滑动的距离;
(2)点C与点O的距离的最大值.
如图,已知AB⊥BD,CD⊥BD.
(1)若AB=16,CD=9,BD=15,请问在BD上是否存在P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?若存在,求BP的长;若不存在,请说明理由;
(2)若AB=16,CD=9,BD=24,请问在BD上存在多少个P点,使以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似?并求BP的长;
(3)若AB=m,CD=n,BD= ,请问在m、n、
,请问在m、n、 满足什么关系时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点?
满足什么关系时,存在以P、A、B三点为顶点的三角形与以P、C、D三点为顶点的三角形相似的三个P点?
(本小题满分6分)如图,在边长为1个单位长、度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点).
(1)将△ABC向左平移1个单位,再向上平移5个单位得到△A1B1C1,请画出△A1B1C1;
(2)请在网格中将△ABC以A为位似中心放大 3倍,得△AB2C2,请画出△AB2C2
如图,以等腰三角形 的一腰
的一腰 为直径的⊙O交底边
为直径的⊙O交底边 于点
于点 ,交
,交 于点
于点 ,连结
,连结 ,并过点
,并过点 作
作 ,垂足为
,垂足为 .根据以上条件写出三个正确结论(除
.根据以上条件写出三个正确结论(除 外)是:
外)是:
(1)___________________________________________________________________________;
(2)___________________________________________________________________________;
(3)___________________________________________________________________________.
如图,□ABCD中,E是CD的延长线上一点,BE与AD交于点F, 。
。
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求□ABCD的面积。
如图,某中学初三(2)班数学活动小组利用周日开展课外实践活动,他们要在湖面上测量建在地面上某塔AB的高度.如图,在湖面上点C测得塔顶A的仰角为45°,沿直线CD向塔AB方向前进18米到达点D,测得塔顶A的仰角为60度.已知湖面低于地平面1米,请你帮他们计算出塔AB的高度.(结果保留根号)
在△ABC中,AD是△ABC的高,矩形EFGH的顶点E、H分别在边AB、AC上,FG在边BC上,且两邻边之比EF:FG=5:9,若AD=16cm,BC=48cm,求矩形EFGH的面积.
(本小题满分10分)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3与x轴交于点A(﹣2,0)和点B,与y轴交于点C,该抛物线的对称轴直线x=1与x轴相交于M.
(1)求抛物线的解析式;
(2)动点P从点A出发沿线段AB以每秒3个单位长度的速度向点B运动,同时动点Q从点B出发沿线段BC以每秒2个单位长度的速度向点C运动,其中一个点到达终点时,另一个点也停止运动.设运动时间为t(秒),当以B、P、Q为顶点的三角形与△BCM相似时,求t的值;
(3)设点E在抛物线上,点F在对称轴上,在(2)的条件下,当点运动停止时,是否存在点E、F,使得以B、Q、E、F为顶点的四边形是平行四边形,如果存在写出点E的坐标,如果不存在,请说明理由.