.(本题12分)
已知抛物线y=ax2+bx+c经过P(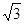 ,3),E(
,3),E(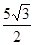 ,0)及原点O(0,0)
,0)及原点O(0,0)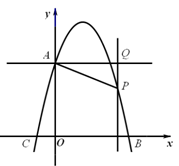
(1)求抛物线的解析式;
(2)过P点作平行于x轴的直线PC交y轴于C点,在抛物线对称轴右侧
且位于直线PC下方的抛物线上,任取一点Q,过点Q作直线QA平行于y
轴交x轴于A点,交直线PC于B点,直线QA与直线PC及两坐标轴围成矩形OABC(如图).是否存在点Q,使得△OPC与△PQB相似?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)如果符合(2)中的Q点在x轴的上方,连接OQ,矩形OABC内的四个三角形△OPC,△PQB,△OQP,△OQA之间存在怎样的关系,为什么?
如图已知二次函数图象的顶点为原点, 直线 的图象与该二次函数的图象交于
的图象与该二次函数的图象交于 点(8,8),直线与
点(8,8),直线与 轴的交点为C,与y轴的交点为B.
轴的交点为C,与y轴的交点为B.
(1)求这个二次函数的解析式与B点坐标;
(2) 为线段
为线段 上的一个动点(点
上的一个动点(点 与
与 不重合),过
不重合),过 作
作 轴的垂线与这个二次函数的图象交于D点,与
轴的垂线与这个二次函数的图象交于D点,与 轴交于点E.设线段PD的长为
轴交于点E.设线段PD的长为 ,点
,点 的横坐标为t,求
的横坐标为t,求 与t之间的函数关系式,并写出自变量t的取值范围;
与t之间的函数关系式,并写出自变量t的取值范围;
(3)在(2)的条件下,在线段 上是否存在点
上是否存在点 ,使得以点P、D、B为顶点的三角形与
,使得以点P、D、B为顶点的三角形与 相似?若存在,请求出
相似?若存在,请求出 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
如图所示,将矩形 沿
沿 折叠,使点
折叠,使点 恰好落在
恰好落在 上
上 处,以
处,以 为边作正方形
为边作正方形 ,延长
,延长 至
至 ,使
,使 ,再以
,再以 、
、 为边作矩形
为边作矩形 .
.试比较
 、
、 的大小,并说明理由.
的大小,并说明理由.令
 ,请问
,请问 是否为定值?若是,请求出
是否为定值?若是,请求出 的值;若不是,请说明理由.
的值;若不是,请说明理由.在(2)的条件下,若
 为
为 上一点且
上一点且 ,抛物线
,抛物线 经过
经过 、
、 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.在(3)的条件下,若抛物线
 与线段
与线段 交于点
交于点 ,试问在直线
,试问在直线 上是否存在点
上是否存在点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似?若存在,请求直线
相似?若存在,请求直线 与
与 轴的交点
轴的交点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
提出问题:如图,有一块分布均匀的等腰三角形蛋糕( ,且
,且 ),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
),在蛋糕的边缘均匀分布着巧克力,小明和小华决定只切一刀将这块蛋糕平分(要求分得的蛋糕和巧克力质量都一样).
背景介绍:这条分割直线即平分了三角形的面积,又平分了三角形的周长,我们称这条线为三角 形的“等分积周线”.
尝试解决: (1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.
(1)小明很快就想到了一条分割直线,而且用尺规作图作出.请你帮小明在图1中画出这条“等分积周线”,从而平分蛋糕.
(2) 小华觉得小明的方法很好,所以自己模仿着在图1中过点C画了一条直线CD交AB于点D.你觉得小华会成功吗?如能成功,说出确定的方法;如不能成功,请说明理由.
(3)通过上面的实践,你一定有了更深刻的认识.请你解决下面的问题:若AB=BC=5 cm,AC=6 cm,请你找出△ABC的所有“等分积周线”,并简要的说明确定的方法.
题背景:如图1,四边形ABCD和CEFG都是正方形,B,C,E在同一条直线上,连接BG,DE.
问题探究:(1)①如图1所示,当G在CD边上时,猜想线段BG、DE的数量关系及所在直线的位置关系.(不要求证明)
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,请选择图2或图3证明你的判断.
类比研究:(2)若将原题中的“正方形”改为“矩形”(如图所示),且
 =k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
=k(其中k>0),请写出 线段BG、DE的数量关系及位置关系.请选择图5或图6证明你的判断(仅证数量关系).
拓展应用:(3)在(1)中图2中,连接DG、BE,若AB=3,EF=2,求BE2+DG2的值.
如图,P为正方形ABCD的对称中心,正方形ABCD的边长为 ,
,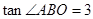 ,直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以
,直线OP交AB于N,DC于M,点H从原点O出发沿x轴的正半轴方向以1个单位每秒速度运动,同时,点R从O出发沿OM方向以 个单位每秒速度运动,运动时间为t,求:
个单位每秒速度运动,运动时间为t,求:
(1)直接写出A、D、P的坐标;
(2)求△HCR面积S与t的函数关系式;
(3)当t为何值时,△ANO与△DMR相似?
(4)求以A、B、C、R为顶点的四边形是梯形时t的值.
如图,在平面直角坐标系中,直角梯形 的边
的边 落在
落在 轴的正半轴上,且
轴的正半轴上,且 ∥
∥ ,
, ,
, =4,
=4, =6,
=6, =8.正方形
=8.正方形 的两边分别落在坐标轴上,且它的面积等于直角梯形
的两边分别落在坐标轴上,且它的面积等于直角梯形 面积。将正方形
面积。将正方形 沿
沿 轴的正半轴平行移动,设它与直角梯形
轴的正半轴平行移动,设它与直角梯形 的重叠部分面积为
的重叠部分面积为 。
。(1)分析与计算:
求正方形 的边长;
的边长;(2)操作与求解:
①正方形 平行移动过程中,通过操作、观察,试判断
平行移动过程中,通过操作、观察,试判断 (
( >0)的变化情况是 ;
>0)的变化情况是 ;
| A.逐渐增大 | B.逐渐减少 | C.先增大后减少 | D.先减少后增大 |
②当正方形 顶点
顶点 移动到点
移动到点 时,求
时,求 的值;
的值;(3)探究与归纳:
设正方形 的顶点
的顶点 向右移动的距离为
向右移动的距离为 ,求重叠部分面积
,求重叠部分面积 与
与 的函数关系式。
的函数关系式。
.在△ABC中,∠C=90°,AC=4cm,BC=5cm,点D在BC上,并且CD=3cm,现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动时间为x秒.(1)用含x的代数式表示AE、DE的长度;
(2)当点Q在线段BD(不包括点B、D)上移动时,设△EDQ的面积为
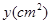 ,求
,求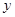 与
与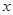 的函数关系式,并写出自变量
的函数关系式,并写出自变量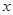 的取值范围;
的取值范围;(3)当
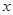 为何值时,△EDQ为直角三角形.
为何值时,△EDQ为直角三角形.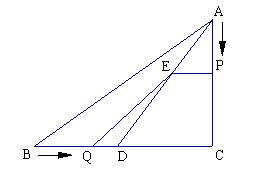
在平面直角坐标系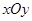 中,抛物线
中,抛物线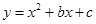 与
与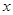 轴交于
轴交于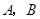 两点(点
两点(点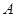 在点
在点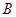 的左侧),与 y 轴交于点
的左侧),与 y 轴交于点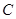 ,点
,点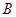 的坐标为(3,0),将直线 y="kx" 沿 y 轴向上平移3个单位长度后恰好经过
的坐标为(3,0),将直线 y="kx" 沿 y 轴向上平移3个单位长度后恰好经过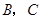 两点.
两点.(1)求直线
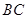 及抛物线的解析式;
及抛物线的解析式;(2)设抛物线的顶点为
 ,点
,点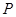 在抛物线的对称轴上,且
在抛物线的对称轴上,且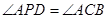 ,求点
,求点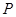 的坐标;
的坐标;(3)连结
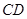 ,求
,求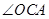 与
与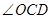 两角和的度数.
两角和的度数.
在平面直角坐标系xOy中,抛物线 与x轴交于A、B两点(点A
与x轴交于A、B两点(点A
在点B的左侧),与y轴交于点C(0 , 4),D为OC的中点.(1)求m的值;
(2)抛物线的对称轴与x轴交于点E,在直线AD上是否存在点F,使得以点A、B、F为顶点的三角形与
 相似?若存在,请求出点F的坐标,若不存在,请说明理由;
相似?若存在,请求出点F的坐标,若不存在,请说明理由; (3)在抛物线的对称轴上是否存在点G,使△GBC中BC边上的高为
 ?若存在,求出点G的坐标;若不存在,请说明理由.
?若存在,求出点G的坐标;若不存在,请说明理由.
在直角坐标系xOy 中,已知某二次函数的图象经过A(-4,0)、B(0,-3),与x轴的正半轴相交于点C,若△AOB∽△BOC(相似比不为1).(1)求这个二次函数的解析式;
(2)求△ABC的外接圆半径r;
(3)在线段AC上是否存在点M(m,0),使得以线段BM为直径的圆与线段AB交于N点,且以点O、A、N为顶点的三角形是等腰三角形?若存在,求出m的值;若不存在,请说明理由.
在Rt 中,
中, ,
, ,
, ,点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于点E.点M在线段AP上,点N在线段BP上,且PM=PN,
,点P是AB边上任意一点,直线PE⊥AB,与边AC或BC相交于点E.点M在线段AP上,点N在线段BP上,且PM=PN, .
.
(1)如图①,当点E与点C重合时,求MP的长;
(2)设
 ,△ENB的面积为y,求y与x的函数关系式,并求出当x取何值时,y有最大值,最大值是多少?
,△ENB的面积为y,求y与x的函数关系式,并求出当x取何值时,y有最大值,最大值是多少?
如图所示,已知抛物线y=x2-1与x轴交于A、B两点,与y轴交于点c.
(1)求A、B、C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
(3)在x轴上方的抛物线上是否存在一点M,过M作MG⊥x轴于点G,使以A、M、G三点为顶点的三角形与△PCA相似.若存在,请求出M点的坐标;否则,请说明理由。
如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折
叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.
(1)求点E、F的坐标(用含m的式子表示);
(2)连接OA,若△OAF是等腰三角形,求m的值;
(3)如图(2),设抛物线
 经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.
经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.
(本题10分)如图,以点M(-1,0)为圆心的圆与y轴、x轴分别交于点A、B、C、D,直线y=- x- 与⊙ M相切于点H,交x轴于点E,交y轴于点F.
M相切于点H,交x轴于点E,交y轴于点F.(1)请
 直接写出OE、⊙M的半径r、CH的长;
直接写出OE、⊙M的半径r、CH的长;(2)如图1,弦HQ交x轴于点P,且DP:PH=3:2,求COS∠QHC的值;
(3)如
 图2,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.
图2,点K为线段EC上一动点(不与E、C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN·MK=a,如果存在,请求出a的值;如果不存在,请说明理由.