初中数学相似多边形的性质选择题

△ABC与△DEF的相似比为3：4，则△ABC与△DEF的周长的比为(    )

A．3：4

B．4：3

C．9：16

D．16：9

如图，为估算学校的旗杆的高度，身高1.6米的小红同学沿着旗杆在地面的影子AB由A向B走去，当她走到点C处时，她的影子的顶端正好与旗杆的影子的顶端重合，此时测得AC=2m，BC=8m，则旗杆的高度是（　　）

A．6.4m

B．7m

C．8m

D．9 m

如图，在△ABC中，点D，E分别在边AB，AC上，DE∥BC，已知AE=6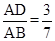， ,则EC的长是（   ）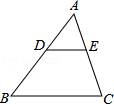

A．4.5

B．8

C．10.5

D．14

如图是小明设计用手电来测量某古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好射到古城墙CD的顶端C处，已知AB⊥BD，CD⊥BD，且测得AB=1.2米，BP=1.8米，PD=12米， 那么该古城墙的高度是（   ）

A．6米

B．8米

C．18米

D．24米

如图，测得BD="120" m，DC="60" m，EC="50" m，则河宽AB为 （  ）．

A．120 m

B．100 m

C．75 m

D．25 m

如图，点A，B，C，D的坐标分别是（1，7），（1，1），（4，1），（6，1），以C，D，E为顶点的三角形与△ABC相似，则点E的坐标不可能是（　　）

A．（6，0）	B．（6，3）
C．（6，5）	D．（4，2）

如图，△ABC中，AE交BC于点D，∠C=∠E，AD=4，BC=8，BD：DC=5：3，则DE的长等于（ ）

A．

B．

C．

D．

如图，梯形ABCD中AD∥BC，对角线AC、BD相交于点O，若AO∶CO＝2∶3，AD＝4，则BC等于(　　)

A．12    B．8    C．7   D．6

如图，在△ABC中，AD，BE是两条中线，则S_△EDC∶S_△ABC＝ (　　)

A．1∶2	B．2∶3
C．1∶3	D．1∶4

如图，正方形ABCD的两边BC，AB分别在平面直角坐标系的x轴、y轴的正半轴上，正方形A′B′C′D′与正方形ABCD是以AC的中点O′为中心的位似图形，已知AC＝3，若点A′的坐标为(1，2)，则正方形A′B′C′D′与正方形ABCD的相似比是(　　)

A．	B．
C．	D．

如图，正方形OABC与正方形ODEF是位似图形，O为位似中心，相似比为1∶，点A的坐标为(1，0)，则E点的坐标为(　　)

A．(，0)	B．
C．(，)	D．(2，2)

如图，在平面直角坐标系中，以原点O为位似中心，将△ABO扩大到原来的2倍，得到△A′B′O.若点A的坐标是(1，2)，则点A′的坐标是(　　)

A．(2，4)	B．(－1，－2)
C．(－2，－4)	D．(－2，－1)

如图所示的两个三角形是位似图形，它们的位似中心是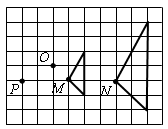

A．点O

B．点P

C．点M

D．点N

下列多边形一定相似的为（    ）

A．两个三角形

B．两个四边形

C．两个正方形

D．两个平行四边形

如图，点D在△ABC的边AC上，要判定△ADB与△ABC相似，添加一个条件，不正确的是

A．∠ABD＝∠C	B．∠ADB＝∠ABC
C．＝	D．＝