如图,在平面直角坐标系中,已知 的三个顶点的坐标分别为 , , .
(1)若 经过平移后得到△ ,已知点 的坐标为 ,写出顶点 , 的坐标;
(2)若 和△ 关于原点 成中心对称图形,写出△ 的各顶点的坐标;
(3)将 绕着点 按顺时针方向旋转 得到△ ,写出△ 的各顶点的坐标.

在平面直角坐标系中, , , 三点坐标分别为 , , .
(1)如图1,顺次连接 , , ,得 .
①点 关于 轴的对称点 的坐标是 ,点 关于 轴的对称点 的坐标是 ;
②画出 关于原点对称的△ ;
③ ;
(2)利用四边形的不稳定性,将第二象限部分由小正方形组成的网格,变化为如图2所示的由小菱形组成的网格,每个小菱形的边长仍为1个单位长度,且较小内角为 ,原来的格点 , , 分别对应新网格中的格点 , , ,顺次连接 , , ,得△ ,则 .

已知:在平面直角坐标系中, 的三个顶点的坐标分别为 , , .
(1)画出 关于原点成中心对称的△ ,并写出点 的坐标;
(2)画出将 绕点 按顺时针旋转 所得的△ .
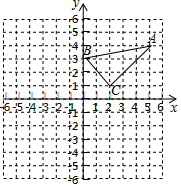
在平面直角坐标系中, 的三个顶点坐标分别为 , ,
(1)画出 关于原点 成中心对称的△ ;
(2)画出△ 关于 轴对称的△ .

已知点 在函数 的图象上,点 在直线 为常数,且 上.若 , 两点关于原点对称,则称点 , 为函数 , 图象上的一对“友好点”.请问这两个函数图象上的“友好点”对数的情况为
A.有1对或2对B.只有1对C.只有2对D.有2对或3对
在平面直角坐标系中,对于平面内任一点 ,若规定以下三种变换:
①△ , , ;
②〇 , , ;
③ , , ,
按照以上变换例如:△ 〇 , , ,则〇 等于 .
已知平行四边形 ABCD的顶点 A在第三象限,对角线 AC的中点在坐标原点,一边 AB与 x轴平行且 AB=2,若点 A的坐标为( a, b),则点 D的坐标为 .
在平面直角坐标系中,点 的坐标是 ,连接 ,将线段 绕原点 旋转 ,得到对应线段 ,则点 的坐标为
| A. |
|
B. |
|
C. |
|
D. |
|
如图,在平面直角坐标系中,
.
(1)将点向右平移3个单位长度,再向上平移1个单位长度,得到点
,则点
的坐标是 .
(2)点与点
关于原点
对称,则点
的坐标是 .
(3)反比例函数的图象经过点,则它的解析式是 .
(4)一次函数的图象经过,
两点,则它的解析式是 .
