如图,平行四边形纸片 的边 , 的长分别是 和 ,将其四个角向内对折后,点 与点 重合于点 ,点 与点 重合于点 .四条折痕围成一个“信封四边形” ,其顶点分别在平行四边形 的四条边上,则 .
如图1,将 纸片沿中位线 折叠,使点 对称点 落在 边上,再将纸片分别沿等腰 和等腰 的底边上的高线 , 折叠,折叠后的三个三角形拼合形成一个矩形,类似地,对多边形进行折叠,若翻折后的图形恰能拼合成一个无缝隙、无重叠的矩形,这样的矩形称为叠合矩形.

(1)将 纸片按图2的方式折叠成一个叠合矩形 ,则操作形成的折痕分别是线段 , ; .
(2) 纸片还可以按图3的方式折叠成一个叠合矩形 ,若 , ,求 的长;
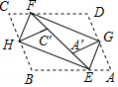
(3)如图4,四边形 纸片满足 , , , , ,小明把该纸片折叠,得到叠合正方形,请你帮助画出叠合正方形的示意图,并求出 、 的长.
如图,对折矩形纸片 ,使 与 重合,得到折痕 ,把纸片展平后再次折叠,使点 落在 上的点 处,得到折痕 , 与 相交于点 .若直线 交直线 于点 , , ,则 的长为
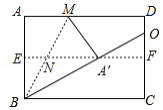
A. B. C. D.
一张矩形纸片 ,已知 , ,小明按如图步骤折叠纸片,则线段 长为

A. B. C.1D.2
如图,在 中,将 沿 折叠后,点 恰好落在 的延长线上的点 处.若 , ,则 的周长为

| A. |
12 |
B. |
15 |
C. |
18 |
D. |
21 |
小红用次数最少的对折方法验证了一条四边形丝巾的形状是正方形,她对折了
A.1次B.2次C.3次D.4次
如图, 中,点 为边 的中点,连接 ,将 沿直线 翻折至 所在平面内,得 ,连接 ,分别与边 交于点 ,与 交于点 .若 , ,则 的长为 .

如图,将长、宽分别为 , 的长方形纸片分别沿 , 折叠,点 , 恰好重合于点 .若 ,则折叠后的图案(阴影部分)面积为

| A. |
|
B. |
|
C. |
|
D. |
|
将一张圆形纸片(圆心为点 沿直径 对折后,按图1分成六等份折叠得到图2,将图2沿虚线 剪开,再将 展开得到如图3的一个六角星.若 ,则 的度数为 .

如图,在 中, , , ,点 在线段 上,且 , 是线段 上的一点,连接 ,把四边形 沿直线 翻折,得到四边形 ,当点 恰好落在线段 上时, .

如图,在 中, , , .
(1)求 边上的高线长.
(2)点 为线段 的中点,点 在边 上,连结 ,沿 将 折叠得到 .
①如图2,当点 落在 上时,求 的度数.
②如图3,连结 ,当 时,求 的长.
