初中数学轴对称-最短路线问题试题

如图，直线l表示石家庄的太平河，点P表示朱河村，点Q表示黄庄村，欲在太平河1上修建一个水泵站（记为点M），分别向两村供水，现有如下四种修建水泵站供水管道的方案，图中实线表示修建的管道，则修建的管道最短的方案是（  ）

如图，在五边形ABCDE中，∠BAE＝136°，∠B＝∠E＝90°，在BC，DE上分别找一点M，N，使得△AMN的周长最小时，则∠AMN＋∠ANM的度数为___________．

（年贵州省遵义市）如图，四边形ABCD中，∠C=，∠B=∠D=，E，F分别是BC，DC上的点，当△AEF的周长最小时，∠EAF的度数为（   ）．

A．

B．

C．

D．

（年贵州省黔南州）如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′；②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是（   ）

A．转化思想               
B．三角形的两边之和大于第三边
C．两点之间，线段最短     
D．三角形的一个外角大于与它不相邻的任意一个内角

（年新疆、生产建设兵团）如图，直线与x轴、y轴分别交于点A、B．抛物线经过A、B，并与x轴交于另一点C，其顶点为P，

（1）求a，k的值；
（2）在图中求一点Q，A．B、C为顶点的四边形是平行四边形，请直接写出相应的点Q的坐标；
（3）抛物线的对称轴上是否存在一点M，使△ABM的周长最小？若存在，求△ABM的周长；若不存在，请说明理由；
（4）抛物线的对称轴是上是否存在一点N，使△ABN是以AB为斜边的直角三角形？若存在，求出N点的坐标，若不存在，请说明理由．

如图， $A$ ， $B$ 两点的坐标分别为 $A(4,3)$ ， $B(0,-3)$ ，在 $x$ 轴上找一点 $P$ ，使线段 $\mathit{PA}+\mathit{PB}$ 的值最小，则点 $P$ 的坐标是 　　．

△ABC在平面直角坐标系xOy中的位置如图所示．

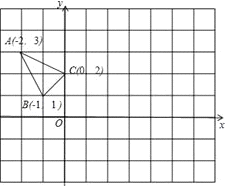
（1）作△ABC关于y轴成轴对称的△A₁B₁C₁；
（2）将△A₁B₁C₁向右平移4个单位，作出平移后的△A₂B₂C₂；则此三角形的面积为       ．
（3）在x轴上求作一点P，使PA₁+PC₂的值最小，点P的坐标为       ．

如图，在 $\text{Rt}\Delta \text{AOB}$中， $\angle \mathit{AOB}=90°$， $\mathit{OA}=4$， $\mathit{OB}=6$，以点 $O$为圆心，3为半径的 $\odot O$，与 $\mathit{OB}$交于点 $C$，过点 $C$作 $\mathit{CD}\perp \mathit{OB}$交 $\mathit{AB}$于点 $D$，点 $P$是边 $\mathit{OA}$上的动点，则 $\mathit{PC}+\mathit{PD}$的最小值为 　　．