如图,直线 与双曲线 相交于 、B两点,在y轴上找一点P,当 的值最小时,点P的坐标为 .

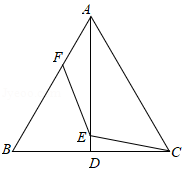
如图,在Rt△ ABC中,∠ C=90°, AC=3, BC=4, D、 E分别是 AB、 BC边上的动点,则 AE+ DE的最小值为( )

| A. |
|
B. |
|
C. |
5 |
D. |
|
如图,菱形 ABCD的边长为2 cm,∠ A=120°,点 E是 BC边上的动点,点 P是对角线 BD上的动点,若使 PC+ PE的值最小,则这个最小值为 .

如图,在周长为12的菱形 中,
中, ,
, ,若
,若 为对角线
为对角线 上一动点,则
上一动点,则 的最小值为
的最小值为


A.1B.2C.3D.4
如图,已知一次函数 的图象与反比例函数 的图象交于点A(﹣1,2)和点B,点C在y轴上.
(1)当△ABC的周长最小时,求点C的坐标;
(2)当 x+b<
x+b< 时,请直接写出x的取值范围.
时,请直接写出x的取值范围.

如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是( )

A.4B. C. D.
如图, 为等边三角形,边长为6, ,垂足为点 ,点 和点 分别是线段 和 上的两个动点,连接 , ,则 的最小值为 .
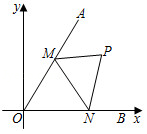
如图,在平面直角坐标系中,已知 , ,在 轴上取两点 , (点 在点 左侧),且始终保持 ,线段 在 轴上平移,当 的值最小时,点 的坐标为 .

如图,等边 的边长为3,点 在边 上, ,线段 在边 上运动, ,有下列结论:
① 与 可能相等;
② 与 可能相似;
③四边形 面积的最大值为 ;
④四边形 周长的最小值为 .
其中,正确结论的序号为

| A. |
①④ |
B. |
②④ |
C. |
①③ |
D. |
②③ |
在平面直角坐标系中的位置如图所示,且
,在
内有一点
,
,
分别是
,
边上的动点,连接
,
,
,则
周长的最小值是 .
在平面直角坐标系中,长为2的线段 (点 在点 右侧)在 轴上移动, , ,连接 , ,则 的最小值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,正方形 的边长为4,点 在 上且 , 为对角线 上一动点,则 周长的最小值为

| A. |
5 |
B. |
6 |
C. |
7 |
D. |
8 |
如图,在矩形中,
,
,点
是边
的中点,反比例函数
的图象经过点
,交
边于点
,直线
的解析式为
.
(1)求反比例函数的解析式和直线
的解析式;
(2)在轴上找一点
,使
的周长最小,求出此时点
的坐标;
(3)在(2)的条件下,的周长最小值是 .
