正如我们小学学过的圆锥体积公式 表示圆周率, 表示圆锥的底面半径, 表示圆锥的高)一样,许多几何量的计算都要用到 .祖冲之是世界上第一个把 计算到小数点后7位的中国古代科学家,创造了当时世界上的最高水平,差不多过了1000年,才有人把 计算得更精确.在辉煌成就的背后,我们来看看祖冲之付出了多少.现在的研究表明,仅仅就计算来讲,他至少要对9位数字反复进行130次以上的各种运算,包括开方在内.即使今天我们用纸笔来算,也绝不是一件轻松的事情,何况那时候没有现在的纸笔,数学计算不是用现在的阿拉伯数字,而是用算筹(小竹棍或小竹片)进行的,这需要怎样的细心和毅力啊!他这种严谨治学的态度,不怕复杂计算的毅力,值得我们学习.
下面我们就来通过计算解决问题:已知圆锥的侧面展开图是个半圆,若该圆锥的体积等于 ,则这个圆锥的高等于
| A. |
|
B. |
|
C. |
|
D. |
|
如图,从一张腰长为 ,顶角为 的等腰三角形铁皮 中剪出一个最大的扇形 ,用此剪下的扇形铁皮围成一个圆锥的侧面(不计损耗),则该圆锥的底面半径为

| A. |
|
B. |
|
C. |
|
D. |
|
(年新疆乌鲁木齐市)圆锥的侧面展开图是一个弧长为12π的扇形,则这个圆锥底面积的半径是( )
| A.24 | B.12 | C.6 | D.3 |
(年蒙自市初中学业水平第一次模拟测试)已知圆锥的底面半径为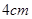 ,母线长为
,母线长为 ,则这个圆锥的侧面积是( )
,则这个圆锥的侧面积是( )
A.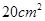 |
B.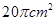 |
C.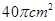 |
D.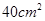 |
在几何体表面上,蚂蚁怎样爬行路径最短?
(1)如图①,圆锥的母线长为 , 为母线 的中点,点 在底面圆周上, 的长为 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点 爬行到点 的最短路径,并标出它的长(结果保留根号).

(2)图③中的几何体由底面半径相同的圆锥和圆柱组成. 是圆锥的顶点,点 在圆柱的底面圆周上,设圆锥的母线长为 ,圆柱的高为 .
①蚂蚁从点 爬行到点 的最短路径的长为 (用含 , 的代数式表示).
②设 的长为 ,点 在母线 上, .圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点 爬行到点 的最短路径的示意图,并写出求最短路径的长的思路.