如图,从一块直径是2的圆形铁片上剪出一个圆心角为 的扇形,将剪下来的扇形围成一个圆锥.那么这个圆锥的底面圆的半径是

| A. |
|
B. |
|
C. |
|
D. |
1 |
用一块弧长 的扇形铁片,做一个高为 的圆锥形工件侧面(接缝忽略不计),那么这个扇形铁片的面积为 .
已知圆锥的母线长为10,高为8,则该圆锥的侧面展开图(扇形)的弧长为 .(用含 的代数式表示),圆心角为 度.
在几何体表面上,蚂蚁怎样爬行路径最短?
(1)如图①,圆锥的母线长为 , 为母线 的中点,点 在底面圆周上, 的长为 .在图②所示的圆锥的侧面展开图中画出蚂蚁从点 爬行到点 的最短路径,并标出它的长(结果保留根号).

(2)图③中的几何体由底面半径相同的圆锥和圆柱组成. 是圆锥的顶点,点 在圆柱的底面圆周上,设圆锥的母线长为 ,圆柱的高为 .
①蚂蚁从点 爬行到点 的最短路径的长为 (用含 , 的代数式表示).
②设 的长为 ,点 在母线 上, .圆柱的侧面展开图如图④所示,在图中画出蚂蚁从点 爬行到点 的最短路径的示意图,并写出求最短路径的长的思路.
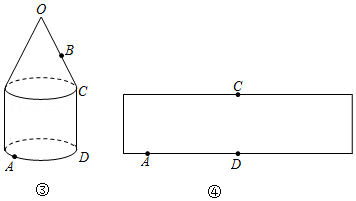
某同学在数学实践活动中,制作了一个侧面积为 ,底面半径为6的圆锥模型(如图所示),则此圆锥的母线长为 .

某种冰激凌的外包装可以视为圆锥,它的底面圆直径 与母线 长之比为 .制作这种外包装需要用如图所示的等腰三角形材料,其中 , .将扇形 围成圆锥时, , 恰好重合.
(1)求这种加工材料的顶角 的大小.
(2)若圆锥底面圆的直径 为 ,求加工材料剩余部分(图中阴影部分)的面积.(结果保留
一个圆柱形橡皮泥,底面积是 .高是 .如果这个橡皮泥的一半,把它捏成高为 的圆锥,则这个圆锥的底面积是 .
如图,要用一个扇形纸片围成一个无底盖的圆锥(接缝处忽略不计),若该圆锥的底面圆周长为 ,侧面积为 ,则这个扇形的圆心角的度数是 度.
