如图,在4×4的正方形网格中,每个小正方形的边长为1,若将△AOC绕点O顺时针旋转90°得到△BOD,则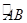 的长为( )
的长为( )

| A.π | B.6π | C.3π | D.1.5π |
在边长为1的方格纸中建立直角坐标系,如图所示,O、A、B三点均为格点.
(1)直接写出线段OB的长;
(2)将△OAB绕点O沿逆时针方向旋转90°得到△OA′B′。请你画出△OA′B′,并求在旋转过程中,点B所经过的路径弧BB′的长度.
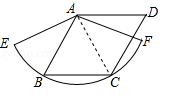
(年贵州省黔南州)如图,边长为1的菱形ABCD的两个顶点B、C恰好落在扇形AEF的弧EF上.若∠BAD=120°,则弧BC的长度等于 (结果保留π).
(年贵州省黔东南州)如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
(1)求证:PN与⊙O相切;
(2)如果∠MPC=30°,PE= ,求劣弧
,求劣弧 的长.
的长.
(年云南省昆明市)如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(记过保留根号和π).
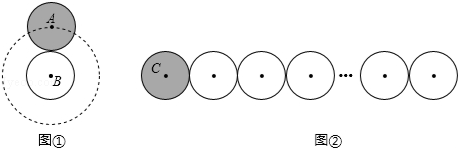
通过对课本中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为 .