初中数学圆内接四边形的性质试题

如图，△ABC中，边BC＝12cm，高AD＝6cm ，边长为x的正方形PQMN的一边在BC上，其余两个顶点分别在AB、AC上，则正方形边长x为（    ）

A．3cm      B．4cm     C．5cm      D．6cm

如图，在平行四边形ABCD中， F是AD延长线上一点，连接BF交DC与点E，则图中相似三角形共有（      ）

A．0对

B．1对

C．2对

D．3对

如图，在长方形ABCD中，AB=3，AD=5，点P在线段BC上运动，现将纸片折叠，使点A与点P重合，得折痕EF（点E、F为折痕与长方形边的交点），设BP=x，当点E落在线段AB上，点F落在线段AD上时，x的取值范围是（   ）

A．2≤x≤ 4

B．1≤x≤4

C．1 ≤x≤3

D．2≤x≤ 3

如图，已知一张长方形纸片ABCD，AB∥CD ，AD=BC=1，AB=CD=5．在长方形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK．

（1）请你动手操作，判断△MNK的形状一定是                  ；
（2）问△MNK的面积能否小于？试说明理由；
（3）如何折叠能够使△MNK的面积最大？请你用备用图探究可能出现的情况，并求最大值．

已知正n边形的每一个内角都等于144°，则n为（ ）

A．9

B．10

C．12

D．15

一个多边形的内角和比它的外角和的3倍少180°，那么这个多边形的边数是（   ）

A．7

B．8

C．9

D．10

如图所示，折叠长方形ABCD的一边AD，使点D落在BC边的点F处，已知AB=8cm，BC=10cm，求EF的长．

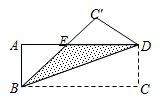
如图，把一张矩形纸片ABCD沿对角线BD折叠，使C点落在C'，且BC'与AD交于E点，若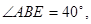则         °

内角和等于外角和2倍的多边形是     边形．

如图，OABC是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴的正半轴上，点C在y轴的正半轴上，OA=10，OC=8，在OC边上取一点D，将纸片沿AD翻折，使点O落在BC边上的点E处，求D、E两点的坐标．

如图，平行四边形ABCD（两组对边平行且相等）的边长AB=4，BC=2，若把它放在直角坐标系内，使AB在x轴上，点C在y轴上，点A的坐标是（-3，0），求点B、C、D的坐标．

已知矩形长和宽分别为4和2，是否存在另一个矩形，它的周长和面积分别是已知矩形的？若存在请计算这个矩形的两边长，若不存在请说明理由．

已知：如图，线段a．求作：正方形ABCD，使正方形ABCD的对角线AC=a．

下列命题是真命题的是（  ）

A．四边都相等的四边形是矩形

B．菱形的对角线相等

C．对角线互相垂直的四边形是正方形

D．对角线相等的菱形是正方形

如图，在正方形ABCD中，E、F分别是边AD、CD上的点，，连接EF并延长交BC的延长线于点G．

（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长．