初中数学圆内接四边形的性质填空题

已知等腰三角形的腰长为5，一腰上的高为4，则以底边为边长的正方形的面积为          ．

将一长方形纸条按如图所示折叠， ∠2=55°，则∠1=__________．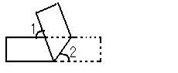

如图，小亮从A点出发前进10m，向右转15°，再前进10m，又向右转15°…… 这样一直走下去，

他第一次回到出发点A时，一共走了         m

如图，正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG，EF与AD相交于点H，延长DA交GF于点K．若正方形ABCD边长为，则AK=           ．

已知正方形ABCD，以CD为边作等边三角形△CDE，则∠AED的度数是            ．

已知菱形的两条对角线长分别为6和8，则菱形的周长是     ，面积是         ．

如图，将长AB=5cm，宽AD=3cm的矩形纸片ABCD折叠，使点A与C重合，折痕为EF，则AE长为           cm．

如图，在△ABC中，∠ABC=90°，BD为AC的中线，过点C作CE⊥BD于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．若AG=13，CF=6，则四边形BDFG的周长为            ．

如图，一张长方形纸片宽AB=8cm，长BC=10cm，现将纸片折叠，使顶点D落在BC边上的点F处（折痕为AE），则EC=      ．

意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为正方形的边长值构造正方形，再分别依次从左到右取2个、3个、4个、5个…正方形拼成如上长方形，若按此规律继续作长方形，则序号为⑦的长方形周长是           ．

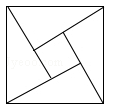
如图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如果大正方形的面积是13，小正方形的面积是1，那么每个直角三角形的周长为          ．

在直角三角形中，两条直角边的长分别是12和5，则斜边上的中线长是___________．

如图，已知AB=CD，AD=CB，且AB∥CD，AD∥BC， AC、BD相交于点O，则图中共有          对全等三角形．

如图，正方形ABCD的边长是4，对角线为，∠DAC的平分线交DC于点E，若点P、Q分别是AD和AE上的动点，则DQ+PQ的最小值_        ．

如图，在平行四边形ABCD中，AD＝5cm， AP＝8cm ， AP平分∠DAB，交DC于点P，过点B作BE⊥AD于点E，BE交AP于点F，则tan∠BFP＝      ．