江苏省扬州市江都区七校联谊八年级上学期期中数学试卷
下面有4个汽车标志图案,其中是轴对称图形的是 ( )

| A.②③④ | B.①②③ | C.①②④ | D.①③④ |
下列说法中,正确的是 ( )
| A.斜边对应相等的两个直角三角形全等 |
| B.底边对应相等的两个等腰三角形全等 |
| C.面积相等的两个等边三角形全等 |
| D.面积相等的两个长方形全等 |
等腰三角形的两边分别为3和6,则这个三角形的周长是 ( )
| A.12 | B.15 | C.9 | D.12或15 |
下列各组线段中,不能作为直角三角形三边的是 ( )
| A.20,21,29 | B.9,12,15 | C.4,5,6 | D.15,8,17 |
到三角形三条边距离相等的点是 ( )
| A.三条角平分线的交点 |
| B.三边中线的交点 |
| C.三边上高所在直线的交点 |
| D.三边的垂直平分线的交点 |
如图,若∠B=∠C,∠1=∠3,则,∠1与∠2之间的关系是 ( )

| A.∠1=2∠2 | B.3∠1-∠2=1800 |
| C.∠1+3∠2=1800 | D.2∠1+∠2=1800 |
如图,三角形ABC中,∠A的平分线交BC于点D,过点D作DE⊥AC,DF⊥AB,垂足分别为E,F,下面四个结论:①∠AFE=∠AEF;②AD垂直平分EF;③ ;④EF∥BC.其中正确的是 ( )
;④EF∥BC.其中正确的是 ( )

A.①②③ B.②③④ C.①③④ D.①②③④
如图所示的正方形网格中,网格线的交点称为格点。已知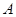 、
、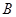 是两格点,如果
是两格点,如果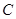 也是图中的格点,且使得
也是图中的格点,且使得 为等腰三角形,则点
为等腰三角形,则点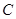 的个数是 个。
的个数是 个。

如图,∠C=90°,AC=10,BC=5,线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问P点运动到 位置时,才能使ΔABC与ΔAPQ 全等。

如图,在△ABC中,∠ABC与∠ACB的平分线交于点E,过点E作MN//BC交AB于点M,交AC于点N,若BM+CN=9,则MN= .

如图,一张长方形纸片宽AB=8cm,长BC=10cm,现将纸片折叠,使顶点D落在BC边上的点F处(折痕为AE),则EC= .

如图,圆柱的底面周长为48 ,高为7
,高为7 ,一只蚂蚁从点
,一只蚂蚁从点 出发沿着圆柱的表面爬行到点
出发沿着圆柱的表面爬行到点 ,现有两种路径:①折线
,现有两种路径:①折线 ;②在圆柱侧面上从
;②在圆柱侧面上从 到
到 的一条最短的曲线
的一条最短的曲线 .请分别计算这两种路径的长,较短的路径是 .(填①或②).
.请分别计算这两种路径的长,较短的路径是 .(填①或②).

已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是 度.

如图,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上.

(1)在图中画出与△ABC关于直线l成轴对称的△A′B′C′;
(2)在直线l上找一点P(在答题纸上图中标出),使PB+PC
的长最短,这个最短长度是 .
如图所示,一根旗杆升旗的绳垂直落地后还剩余1米,若将绳子拉直,则绳端离旗杆底端的距离(BC)有5米.求旗杆的高度.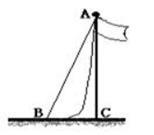
.如图,在△ABC中,点E在AB上,点D在BC上,BD=BE,∠BAD=∠BCE,AD与CE相交于点F,试判断△AFC的形状,并说明理由.
如图,在等腰RT△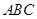 中,
中, ,
,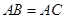 ,点
,点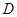 是斜边
是斜边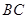 的中点,点
的中点,点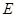 、
、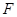 分别为
分别为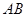 、
、 边上的点,且
边上的点,且 .
.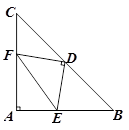
(1)判断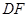 与
与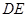 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)若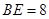 ,
,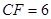 ,求△
,求△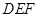 的面积.
的面积.
如图,△ 是等边三角形,点
是等边三角形,点 、
、 分别是
分别是 、
、 的延长线上的点,且
的延长线上的点,且 ,
, 的延长线交
的延长线交 于点
于点 .
.
(1)求证: ;
;
(2)求 的度数.
的度数.
如图,已知直线l1∥l2∥l3,且l1,l2之间的距离为1, l2,l3之间的距离为2 ,点A、C分别在直线l2,l1上,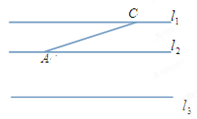
(1)利用直尺和圆规作出以AC为底的等腰△ABC,使得点B落在直线l3上(保留作图痕迹,不写作法);
(2)若(1)中得到的△ABC为等腰直角三角形,求AC的长.
 的值等于 ( )
的值等于 ( )
 或
或
 的平方根是 .
的平方根是 . ,则
,则 = .
= . ,
, ,
, ,
, ,
,  .则阴影部分的面积= .
.则阴影部分的面积= .
 分)计算:
分)计算:

 分)求下面各式中的
分)求下面各式中的 :
: 

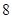 分)已知
分)已知 和
和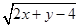 互为相反数,求x+4y的平方根。
互为相反数,求x+4y的平方根。
 粤公网安备 44130202000953号
粤公网安备 44130202000953号