如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
(1)当PE⊥AB,PF⊥BC时,如图1,则 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3, 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
如图,在△ABC中,CD是AB边上的中线,F是CD的中点,过点C作AB的平行线交BF的延长线于点E,连接AE.
(1)求证:EC=DA;
(2)若AC⊥CB,试判断四边形AECD的形状,并证明你的结论.
(本题6分)你能把如图①所示的长方形分成2个全等图形吗?把如图②所示的三角形分成3个全等三角形吗?把如图③所示的长方形分成4个全等三角形吗?
已知:如图,点E,F是□ABCD中AB,DC边上的点,且AE=CF,联结DE,BF.
求证:DE =BF.
如图,在▱ABCD中,AE⊥BC,交边BC于点E,点F为边CD上一点,且DF=BE.过点F作FG⊥CD,交边AD于点G.求证:DG=DC.
如图,纸上有五个边长为1的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.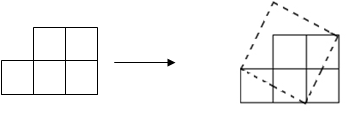

(1)拼成的正方形的面积与边长分别是多少?
(2)如图所示,以数轴的单位长度的线段为边作一个直角三角形,以数轴的-1点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点A,那么点A表示的数是多少?点A表示的数的相反数是多少?
(3)你能把十个小正方形组成的图形纸,剪开并拼成正方形吗?若能,请画出示意图,并求它的边长
已知:如图①,在矩形ABCD中,AB=5,AD= ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).当点F分别平移到线段AB.AD上时,直接写出相应的m的值.
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AD交于点P,与直线BD交于点Q.是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时DQ的长;若不存在,请说明理由.
如图所示,在菱形ABCD中,AB=4,∠BAD=120°,△AEF为正三角形,点E、F分别在菱形的边BC、CD上滑动,且E、F不与B、C、D重合.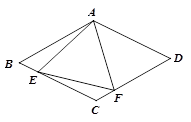
(1)证明不论E、F在BC.CD上如何滑动,总有BE=CF;
(2)当点E、F在BC.CD上滑动时,分别探讨四边形AECF的面积和△CEF的周长是否发生变化?如果不变,求出这个定值;如果变化,求出最小值.
(1)如图1,已知△ABC,以AB、AC为边向△ABC外作等边△ABD和等边△ACE,连接BE,CD,请你完成图形(尺规作图,保留作图痕迹),并猜想BE与CD的关系:___________;你是通过证明_______________ 得到的。
(2)如图2,已知△ABC,以AB、AC为边向外作正方形ABFD和正方形ACGE,连接BE,CD,BE与CD有什么数量关系?并说明理由;
(3)运用(1)、(2)解答中所积累的经验和知识,完成下题:
如图3,要测量池塘两岸相对的两点B,E的距离,已经测得∠ABC=45°,∠CAE=90°,AB=BC=100米,AC=AE,求BE的长.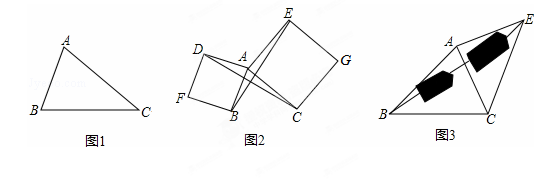
如图,将长方形ABCD沿着对角线BD折叠,使点C落在C′处,BC′交AD于点E.
(1)试判断△BDE的形状,并说明理由;
(2)若AB=4,AD=8,求△BDE的面积.
如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:
(1)在图①中画一条线段MN,使MN= ;
;
(2)在图②中画一个△ABC,使其三边长分别为3, ,
, .
.