初中数学圆内接四边形的性质选择题

若正方形的对角线长为2 cm，则这个正方形的面积为（    ）

A．4

B．2

C．

D．

如图，在矩形ABCD中，AB=1，BC=2，将其折叠，使AB边落在对角线AC上，得到折痕AE，则点E到点B的距离为（    ）              

A．

B．

C．

D．

已知正方形ABCD的一条对角线长为2，则它的面积是（    ）

A．2

B．4

C．6

D．12

一个多边形的内角是1980°，则这个多边形的边数是（    ） 

A．11

B．13

C．9

D．10

顺次连接一个四边形各边的中点所得的新四边形是（       ）

A．平行四边形

B．菱形

C．矩形

D．正方形

一个正多边形的外角与它相邻的内角之比为1：4，那么这个多边形的边数为--（ ）

A．8

B．9

C．10

D．12

如图，△ABC为等腰三角形，如果把它沿底边BC翻折后，得到△DBC，那么四边形ABDC为（ ）

A．

菱形

B．

正方形

C．

矩形

D．

一般平行四边形

如图，菱形ABCD的对角线AC，BD相交于点O，AC=8，BD=6，以AB为直径作一个半圆，则图中阴影部分的面积为（  ）

A．25π-6

B．π-6

C．π-6

D．π-6

如图，是我国古代数学家赵爽的《勾股圆方图》，它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形．如果大正方形的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长的直角边为b，那么（a+b）²的值为（     ）

A．169

B．25

C．19

D．13

若一个多边形的内角和90 0°，则这个多边形的边数为（    ）

A．5

B．7

C．9

D．12

一个多边形的内角和是外角和的2倍，则这个多边形是（   ）

A．四边形

B．五边形

C．六边形

D．八边形

如图，矩形纸片ABCD，AB=3，AD=5，折叠纸片，使点A落在BC边上的E处，折痕为PQ，当点E在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点E在BC边上可移动的最大距离为（ ）

A．1             B．2             C．4                 D．5

下列结论中，平行四边形不一定具备的是（　　）

A．对角相等

B．对角互补

C．邻角互补

D．内角和是360°

设三角形的三边长分别等于下列各数，能构成直角三角形的是（ ）

A．2，4，6	B．4，5，6
C．5，6，10	D．6，8，10

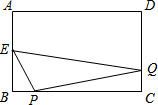
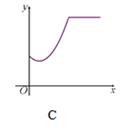
如图，在矩形ABCD中，AB＝4，BC＝6，E为AB中点，动点P从点B开始沿BC方向运动到点C停止，动点Q从点C开始沿CD—DA方向运动，点Q与点P同时出发，当有一个动点到达终点时，两点的运动同时停止．这两点的运动速度均为每秒1个单位．若设他们的运动时间为x（秒），△EPQ的面积为y，则y与x之间的函数关系的图像大致是(      )